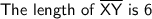Question

What is the length of line xy (the first answer is already there)

giving 100 points btw

Answer 1

`\sf \textsf{ Segment of bisector $\sf \overline{XY} $ = line n }`

`\textsf{The length of }\sf \overline{XY} = 6`

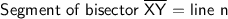
Explanation:

A segment bisector is a line, ray, or segment that divides a line segment into two segments with equal lengths.

The point that divides the line segment into two segments with equal lengths is called the midpoint of the line segment.

In this case:

A segment bisector is line n because it divides line XY into XM and MY equally.

`\textsf{ So, the segment bisector of $ \overline{\textsf{XY}}$ is line n.}`

Again.

Since the segment bisector divides a line segment into two segments with equal lengths.

So,

`\overline{\sf MX} = \overline{\sf MY}`

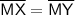
Substituting Value

5x+8 = 9x + 12

Subtract 5x and 12 on both sides

`\sf 5x + 8 -5x -12 = 9x + 12 -5x -12`

Simplify

`\sf -4 = 4x`

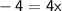
Divide both sides by 4.

`\sf (-4)/(4) =(4x)/(4)`

`\sf x = -1.`

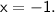
Now,

`\begin{aligned} \textsf{The length of }\overline{XY} & \sf = 5x+8 +9x+ 12\\& \textsf{ Substitute the value of x} \\&=\sf 5* -1 +8 + 9* -1 + 12\\&\textsf{ Simplify} \\ & = \sf -5 +8 -9+12\\ &\sf = 6 \end{aligned}`

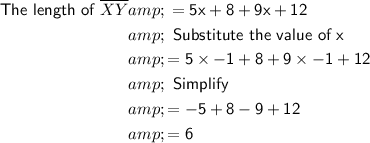
Therefore,

`\textsf{The length of }\sf \overline{XY} \textsf{ is } 6`