Question

N

Challenge You are given the numbers, 37 + n,
{37 + n.
natural numbers.
√n +144
Find the smallest value of n so that all of the numbers in the set are
The smallest value of n that makes all of the numbers in set natural numbers is

Answer 1

Answer: 25

Work Shown

12^2 = 144

13^2 = 169

169 - 144 = 25

If n = 25, then
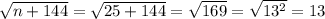`√(n+144) = √(25+144) = √(169) = √(13^2) = 13` which is a natural number.

Also, if n = 25, then
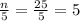`(n)/(5) = (25)/(5) = 5` is also a natural number.

n = 25 is the smallest such number so that each expression results in a natural number. This is because 13^2 = 169 is the next largest perfect square compared to 12^2 = 144. Any other larger perfect squares will require larger values of n.

Other values of n that make each expression a natural number are:

n = 25, n = 145, n = 180, n = 340

There are likely infinitely many other such values of n.