Answer:
Volume of the balloon would be approximately
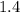 times the value at sea level, assuming that the content of the balloon behaves like an ideal gas.
times the value at sea level, assuming that the content of the balloon behaves like an ideal gas.
Step-by-step explanation:
Assume that the gas in the balloon is an ideal gas. The ideal gas equation would hold:
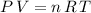 ,
,
Where:
 is the pressure of the gas,
is the pressure of the gas,
 is the volume of the gas,
is the volume of the gas,
 is the quantity of particles in the gas,
is the quantity of particles in the gas,
 is the ideal gas constant, and
is the ideal gas constant, and
 is the temperature of the gas, as measured on an absolute scale such as the Kelvin scale.
is the temperature of the gas, as measured on an absolute scale such as the Kelvin scale.
This question implies that the quantity
 of gas particles in this balloon stays the same. Let
of gas particles in this balloon stays the same. Let
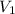 ,
,
 , and
, and
 denote the volume, pressure, and temperature at sea level, and let
denote the volume, pressure, and temperature at sea level, and let
 ,
,
 , and
, and
 denote the new values of these quantities.
denote the new values of these quantities.
The goal is to find the ratio
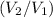 representing the new volume of the balloon relative to the initial volume. Apply the following steps to find this ratio:
representing the new volume of the balloon relative to the initial volume. Apply the following steps to find this ratio:
- Rearrange the ideal gas equation to find the relationship between
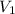 ,
,
 ,
,
 ,
,
 ,
,
 , and
, and
 .
. - Rearrange the relation from the previous step to find an expression for the ratio
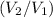 in terms of
in terms of
 ,
,
 ,
,
 , and
, and
 .
. - Ensure that temperatures are measured in degrees Kelvins (an absolute scale for temperature.) Substitute the values into the expression from the previous step and evaluate to find the value of
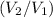 .
.
At the initial pressure and temperature, the ideal gas equation would be:
 .
.
Rearrange to obtain:
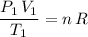 .
.
Similarly, under the new pressure and temperature, this equation becomes:
 .
.
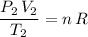 .
.
Assuming that the quantity of gas particles in this balloon stays the same. The value of
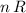 would stay constant regardless of the value of
would stay constant regardless of the value of
 and
and
 . Hence:
. Hence:
 .
.
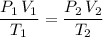 .
.
Rearrange the equation above to find an expression for the ratio
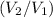 :
:
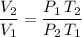 .
.
To find the temperature on the Kelvin scale, add (approximately)
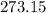 to the value of temperature on the celsius scale:
to the value of temperature on the celsius scale:
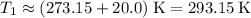 .
.
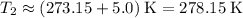 .
.
The pressure at sea level is
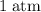 . Thus:
. Thus:
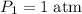 . Given that
. Given that
 :
:
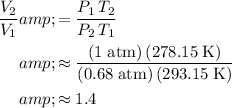 .
.
In other words, the new volume would be approximately
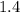 times that at the sea level.
times that at the sea level.