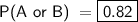Question

What is the probability that either event will occur?

9
A
23
B
18
P(A or B) = P(A) + P(B)
P(A or B) = [?]
Enter as a decimal rounded to the nearest hundredth.

Answer 1

`\sf \textsf{P(A or B) }= \boxed{\sf 0.82 }`

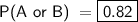
Explanation:

Note:

Probability is defined as the likelihood of an event happening. It is a number between 0 and 1, where 0 means the event is impossible and 1 means the event is certain.

The formula for probability is:

`\sf P(E) = (n(E) )/( n(S))`

where:

• P(E) is the probability of event E happening
• n(E) is the number of favorable outcomes for event E
• n(S) is the total number of possible outcomes

In this case:

Given:

• n(A) = 23
• n(B) = 18
• n(T) = 23+18+9 = 50

To find:

`\sf \textsf{P(A or B) }= P(A)+P(B) = ?`

Solution:

Let's find the probability of A: P(A)

Using the above formula:

`\sf P(A) = (n(A))/(n(T))`

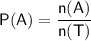
Substituting value:

`\sf P(A) = (23)/(50)`

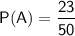
Similarly

Let's find the probability of B: P(B)

Using the above formula:

`\sf P(B) = (n(B))/(n(T))`

Substituting value:

`\sf P(B) = (18)/(50)`

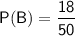
Since we have,

`\sf \sf \textsf{P(A or B) }= P(A)+P(B)`

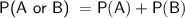
Substitute value of P(A) and P(B)

`\sf \sf \textsf{P(A or B) }=(23)/(50)+(18)/(50)`

Simplify:

`\sf \sf \textsf{P(A or B) }=(23+18)/(50)`

`\sf \textsf{P(A or B) }=(41)/(50)`

`\sf \sf \textsf{P(A or B) }\approx 0.82`

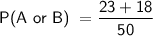
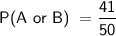
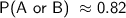
Therefore,

`\sf \textsf{P(A or B) }= \boxed{\sf 0.82 }`