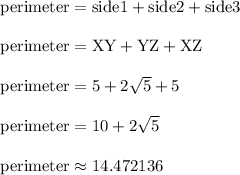Question

Find the perimeter of the polygon with the given vertices. X(- 1, 3), Y(3, 0), Z(-1, -2)

Answer 1

Exact perimeter =
`10+2√(5)`

Approximate perimeter = 14.472136

Round the approximate value however needed.

=====================================================

Step-by-step explanation

We need to know how far it is from point X to point Y.

Use the distance formula.

`(x_1,y_1) = (-1,3) \text{ and } (x_2, y_2) = (3,0)\\\\d = √((x_1 - x_2)^2 + (y_1 - y_2)^2)\\\\d = √((-1-3)^2 + (3-0)^2)\\\\d = √((-4)^2 + (3)^2)\\\\d = √(16 + 9)\\\\d = √(25)\\\\d = 5\\\\`

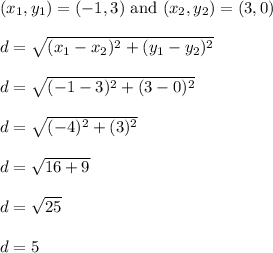
The distance from point X(-1,3) to point Y(3,0) is exactly 5 units.

Therefore, segment XY is 5 units long.

Let's find the distance from Y to Z.

`(x_1,y_1) = (3,0) \text{ and } (x_2, y_2) = (-1,-2)\\\\d = √((x_1 - x_2)^2 + (y_1 - y_2)^2)\\\\d = √((3-(-1))^2 + (0-(-2))^2)\\\\d = √((3+1)^2 + (0+2)^2)\\\\d = √((4)^2 + (2)^2)\\\\d = √(16 + 4)\\\\d = √(20)\\\\d = √(4*5)\\\\d = √(4)*√(5)\\\\d = 2√(5)\\\\d \approx 4.472136\\\\`

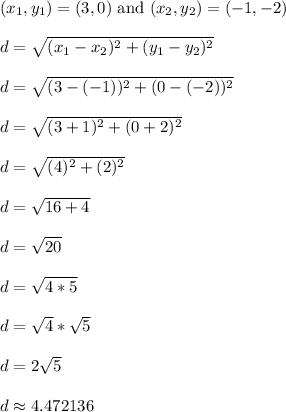
The length of segment YZ is exactly
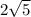`2√(5)` units which approximates to roughly 4.472136 units.

Then we'll need the distance from X to Z.

`(x_1,y_1) = (-1,3) \text{ and } (x_2, y_2) = (-1,-2)\\\\d = √((x_1 - x_2)^2 + (y_1 - y_2)^2)\\\\d = √((-1-(-1))^2 + (3-(-2))^2)\\\\d = √((-1+1)^2 + (3+2)^2)\\\\d = √((0)^2 + (5)^2)\\\\d = √(0 + 25)\\\\d = √(25)\\\\d = 5\\\\`

Or as a quick shortcut, notice how the x coordinates are the same (both are -1). This means we just need to subtract the y coordinates and apply absolute value to ensure the result is positive. Another way is to count the number of spaces between -2 and 3 on the number line.

----------------

Here's a summary of each side length

`XY = 5\\\\YZ = 2√(5) \approx 4.472136\\\\XZ = 5`

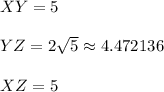
We have an isosceles triangle because exactly two sides are the same length.

The perimeter is then found by adding up those sides:

`\text{perimeter} = \text{side1}+\text{side2}+\text{side3}\\\\\text{perimeter} = \text{XY}+\text{YZ}+\text{XZ}\\\\\text{perimeter} = 5+2√(5)+5\\\\\text{perimeter} = 10+2√(5)\\\\\text{perimeter} \approx 14.472136\\\\`