Question

Formulate but do not solve the problem.

Mr. and Mrs. Garcia have a total of $175,000 to be invested in stocks, bonds, and a money market account. The stocks have a rate of return of 11%/year, while the bonds and the money market account pay 9%/year and 3%/year, respectively. The Garcias have stipulated that the amount invested in the money market account should be equal to the sum of 20% of the amount invested in stocks and 25% of the amount invested in bonds. How should the Garcias allocate their resources if they require an annual income of $15,000 from their investments? (Let x, y, and z denote the amount, in dollars, in stocks, bonds, and money markets, respectively.)

Answer 1

`\begin{cases}\text{x}+\text{y}+\text{z} = 175000\\0.11\text{x}+0.09\text{y}+0.03\text{z} = 15000\\\text{z} = 0.20\text{x} + 0.25\text{y}\end{cases}`

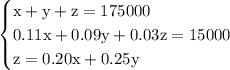
Step-by-step explanation

• x = amount invested in stocks
• y = amount invested in bonds
• z = amount invested in money markets

Each amount is in dollars. The variables x,y,z are nonnegative.

The total of those three groups gives the first equation x+y+z = 175000

The second equation 0.11x+0.09y+0.03z = 15000 is the idea where stocks return 11%, bonds 9%, and money markets return 3%. Those subtotals are then required to return a grand total of $15000. This is over a one year period.

The third equation is from the info that "the amount invested in the money market account should be equal to the sum of 20% of the amount invested in stocks and 25% of the amount invested in bonds"

z = 20% of stocks + 25% of bonds

z = 20% of x + 25% of y

z = 0.20x + 0.25y