Question

Find and equation for each line in the form ax+by=c, where a,b and c are integers with no factor common to all three and a is greater than or equal to 0.

x-intercept -6, y-intercept -3

Answer 1

Answer: x + 2y = -6

=================================================

Step-by-step explanation

The x-intercept occurs when x = -6 and y = 0. The y coordinate of the x-intercept is always zero.

The y-intercept always occurs when x = 0. The location of the y-intercept is (0,-3)

Let's find the slope of the line through (-6,0) and (0,-3)

`(x_1,y_1) = (-6,0) \text{ and } (x_2,y_2) = (0,-3)\\\\m = \text{slope} = \frac{\text{rise}}{\text{run}} = \frac{\text{change in y}}{\text{change in x}}\\\\m = \frac{\text{y}_(2) - \text{y}_(1)}{\text{x}_(2) - \text{x}_(1)}\\\\m = (-3 - 0)/(0 - (-6))\\\\m = (-3 - 0)/(0 + 6)\\\\m = (-3)/(6)\\\\m = -(1)/(2)\\\\`

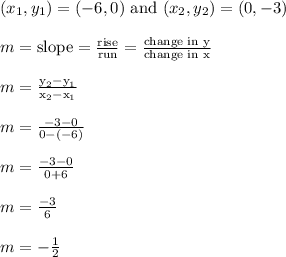
We arrive at the slope-intercept form y = (-1/2)x - 3

slope = -1/2

y intercept = -3

Compare this to the template y = mx+b

--------------

The next step is to convert from slope-intercept form to standard form.

y = (-1/2)x - 3

2y = 2*( (-1/2)x - 3 )

2y = -x - 6

x + 2y = -6

This is in the format ax+by = c where: a = 1, b = 2, c = -6

In this case a > 0. If a < 0, then we'd have to multiply both sides by -1 to flip the sign.