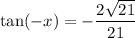Question

Please help with an explanation !!

Answer 1

`\text{a)} \quad \cos\left((\pi)/(2)-x\right)=(2)/(5)`

`\text{b)} \quad \cos(\pi - x)=-(√(21))/(5)`

`\text{c)} \quad \sin \left(\pi + x\right)=-(2)/(5)`

`\text{d)}\quad \tan(-x)=-(2√(21))/(21)`

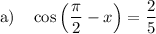
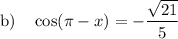
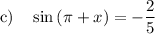
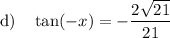
Explanation:

Given:

`\sin(x)=(2)/(5)\;\;\text{for}\;\;0\leq x \leq (\pi)/(2)`

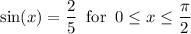
To find cos(x), use the Pythagorean identity sin²(x) + cos²(x) = 1.

Substitute in sin(x) = 2/5, and solve for cos(x):

`\begin{aligned}\left((2)/(5)\right)^2+\cos^2(x)&=1\\\\\cos^2(x)&=1-\left((2)/(5)\right)^2\\\\\cos^2(x)&=1-(4)/(25)\\\\\cos^2(x)&=(25)/(25)-(4)/(25)\\\\\cos^2(x)&=(21)/(25)\\\\\cos(x)&=\pm \sqrt{(21)/(25)}\\\\\cos(x)&=\pm (√(21))/(5)\end{aligned}`

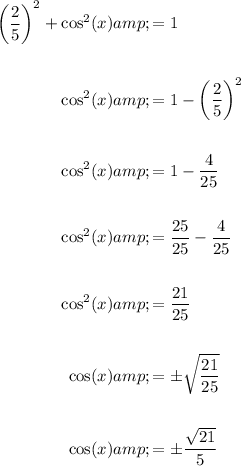
Since x is in the first quadrant (0 ≤ x ≤ π/2), cos(x) is positive, so:

`\cos(x)=(√(21))/(5)`

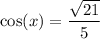
To find tan(x), use the identity tan(x) = sin(x) / cos(x):

`\tan(x)=((2)/(5))/((√(21))/(5))\\\\\\\tan(x)=(2)/(√(21))\\\\\\\tan(x)=(2√(21))/(21)`

`\hrulefill`

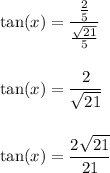
Question (a)

To find cos(π/2 - x), we can use the cofunction trigonometric identity:

`\boxed{\cos\left((\pi)/(2)-x\right)=\sin(x)}`

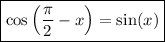
As sin(x) = 2/5, then:

`\cos\left((\pi)/(2)-x\right)=(2)/(5)`

`\hrulefill`

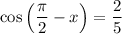
Question (b)

To find cos(π - x), we can use the Cosine Difference formula:

`\boxed{\cos(A-B)=\cos A\cos B+\sin A\sin B}`

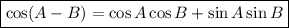
Let A = π and B = x. Therefore:

`\cos(\pi-x)=\cos \pi \cos x + \sin \pi \sin x`

As cos π = -1 and sin π = 0:

`\cos(\pi-x)=(-1)\cdot \cos x + 0\cdot \sin x`

`\cos(\pi-x)=-\cos x`

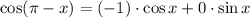
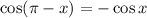
From our previous calculations, cos(x) = √(21) / 5. Therefore:

`\cos(\pi - x)=-(√(21))/(5)`

`\hrulefill`

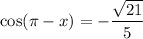
Question (c)

To find sin(π + x), we can use the Sine Sum formula:

`\boxed{\sin(A+B)=\sin A\cos B+\cos A\sin B}`

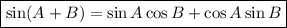
Let A = π and B = x. Therefore:

`\sin(\pi+x)=\sin\pi \cos x + \cos\pi \sin x`

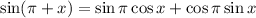
As sin π = 0 and cos π = -1:

`\sin(\pi+x)=0 \cdot \cos x + (-1) \cdot \sin x`

`\sin(\pi+x)=- \sin x`

As sin(x) = 2/5, then:

`\sin \left(\pi + x\right)=-(2)/(5)`

`\hrulefill`

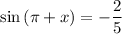
Question (d)

To find tan(-x), we can use the Odd Trigonometric Function:

`\boxed{\tan(-x)=-\tan(x)}`

From our previous calculations, tan(x) = (2√(21)) / 21. Therefore:

`\tan(-x)=-(2√(21))/(21)`