Question

What is the perimeter of a polygon with the vertices (-10,-4), (-2,1), (-5,4)

Answer 1

Perimeter =
`3√(2) +2√(89)`

Explanation:

The perimeter of a shape is the sum of the sides or circumference if we're talking about a circle

In this case, the polygon is a isosceles triangle meaning that it has 2 congruent sides

To find the perimeter of the polygon, we're going to find the distance between all sides

Step 1. Find the distance between (-2, 1) and (-5, 4)

But first, we need to know what the distance formula is. The distance formula is
`d=√((x_2-x_1)^2+(y_2-y_1)^2)` where
`x_1,y_1` are the coordinates of the first point and
`x_2,y_2` are the coordinates of the second point.

`d=√((-5-(-2))^2+(4-1)^2)`

`d=√((-3)^2+(3)^2)`

`d=√(9+9)`

`d=√(18)`

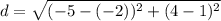
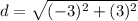
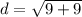
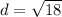
We can actually further simplify
`√(18)` by using 2 of its factors (9 and 2) and square rooting the perfect square number which is 9 and leaving that outside of the radical and placing the 2 inside the radical.

`d=3√(2)`

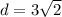
The distance between (-2, 1) and (-5, 4) is
`3√(2)`

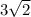
Step 2. Find the distance between (-5, 4) and (-10, -4)

`d=√((x_2-x_1)^2+(y_2-y_1)^2)`

`d=√((-10-(-5))^2+(-4-4)^2)`

`d=√((-5)^2+(-8)^2)`

`d=√(25+64)`

`d=√(89)`

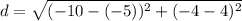
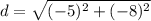
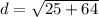
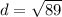
The distance between (-5, 4) and (-10, -4) is
`√(89)`

Step 3. Find the distance between (-10, -4) and (-2, 1)

`d=√((x_2-x_1)^2+(y_2-y_1)^2)`

`d=√((-2-(-10))^2+(1-(-4))^2)`

`d=√((8)^2+(5)^2)`

`d=√(64+25)`

`d=√(89)`

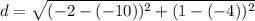
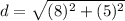
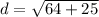
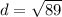
The distance between (-10, -4) and (-2, 1) is
`√(89)`

Last step is to Add the Distance Between All the points

`3√(2) +√(89) +√(89) =3√(2) +2√(89)`

The perimeter of the polygon is
`3√(2) +2√(89)`