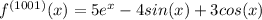Answer: 5eˣ - 4sin(x) + 3cos(x)
Explanation:
We know the special derivatives of the trigonometric functions sine and cosine, and we will use those to find our answer.
The first derivative of sin(x) is cos(x). The second derivative of sin(x) is -sin(x), since that is the derivative of cos(x). The third derivative of sin(x) is -cos(x), since the derivative of sin(x) is cos(x), then multiplied by -1. The fourth derivative of sin(x) is sin(x).
The first derivative of cos(x) is -sin(x). The second derivative of cos(x) is -cos(x). The third derivative of cos(x) is sin(x). The fourth derivative of cos(x) is cos(x).
Since both derivatives loop around at the fourth derivative, we can easily calculate the result of higher derivatives of sine and cosine. To find the higher derivatives, we can take the number of the derivative and divide it by 4, then find the remainder, or, in the case of this problem, 1001 mod 4.
If the remainder is 0, the derivative will match the fourth derivative. If it is 1, it will match the first derivative. If it is 2, it will follow the second derivative. If it is 3, it will follow the third derivative.
When we divide 1001 by 4, the remainder is 1 (1001 mod 4 is 1). Therefore, the 1001th derivative of sine and cosine is equal to the first derivative.
So, the 1001th derivative of 3sin(x) is 3cos(x) and the 1001th derivative of 4cos(x) is -4sin(x).
Note the coefficients are not affected by derivatives since they are constant coefficients.
The derivative of eˣ is always eˣ, so the 1001th derivative of 5eˣ is just 5eˣ .
Putting this all together, we have