Question

1. solve triangle PQR if: P = 40; Q = 90° and QR = 62 units

2. solve triangle DEF if: E = 90°; DE = 64 and DF = 81,7

Answer 1

Question 1:

• P = 40°
• Q = 90°
• R = 50°
• PQ = 73.9 units
• QR = 62 units
• PR = 96.5 units

Question 2:

• D = 38.4°
• E = 90°
• F = 51.6°
• DE = 64 units
• EF = 50.8 units
• DF = 81.7 units

Explanation:

Question 1

Given values of triangle PQR:

• P = 40°
• Q = 90°
• QR = 62 units

The angle sum property of a triangle states that the sum of the angles in a triangle is always 180°. Therefore:

`\begin{aligned}Q + P + R &= 180^(\circ)\\90^(\circ) + 40^(\circ) + R &= 180^(\circ)\\130^(\circ) + R& = 180^(\circ)\\R &= 180^(\circ) - 130^(\circ)\\R &= 50^(\circ)\end{aligned}`

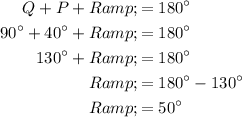
So, R = 50°.

In triangle PQR:

• Side QR is opposite angle P.
• Side PQ is opposite angle R.
• Side PR is opposite angle Q.

To find the side lengths PQ and PR, use the Law of Sines.

`\boxed{\begin{minipage}{7.6 cm}\underline{Law of Sines} \\\\$(a)/(\sin A)=(b)/(\sin B)=(c)/(\sin C)$\\\\\\where:\\ \phantom{ww}$\bullet$ $A, B$ and $C$ are the angles. \\ \phantom{ww}$\bullet$ $a, b$ and $c$ are the sides opposite the angles.\\\end{minipage}}`

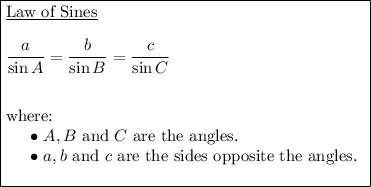
For triangle PQR:

`(QR)/(\sin P)=(PR)/(\sin Q)=(PQ)/(\sin R)`

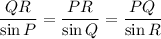
Substitute the known values into the equation:

`(62)/(\sin 40^(\circ))=(PR)/(\sin 90^(\circ))=(PQ)/(\sin 50^(\circ))`

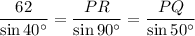
Solve for PR:

`\begin{aligned}(62)/(\sin 40^(\circ))&=(PR)/(\sin 90^(\circ))\\\\PR&=(62\sin 90^(\circ))/(\sin 40^(\circ))\\\\PR&=96.4548772...\\\\PR&=96.5\; \sf units\;(nearest\;tenth)\end{aligned}`

Solve for PQ:

`\begin{aligned}(62)/(\sin 40^(\circ))&=(PQ)/(\sin 50^(\circ))\\\\PQ&=(62\sin 50^(\circ))/(\sin 40^(\circ))\\\\PQ&=73.8887227...\\\\PQ&=73.9\; \sf units\;(nearest\;tenth)\end{aligned}`

Therefore:

• P = 40°
• Q = 90°
• R = 50°
• PQ = 73.9 units
• QR = 62 units
• PR = 96.5 units

`\hrulefill`

Question 2

Given values of triangle DEF:

• E = 90°
• DE = 64 units
• DF = 81.7 units

In triangle DEF:

• Side DE is opposite angle F.
• Side EF is opposite angle D.
• Side DF is opposite angle E.

As triangle DEF is a right triangle, where angle E is the right angle, this means the side DF is the hypotenuse and side DE is one of the legs.

To find the length of the other leg (EF), we can use Pythagoras Theorem.

`\boxed{\begin{minipage}{9 cm}\underline{Pythagoras Theorem} \\\\$a^2+b^2=c^2$\\\\where:\\ \phantom{ww}$\bullet$ $a$ and $b$ are the legs of the right triangle. \\ \phantom{ww}$\bullet$ $c$ is the hypotenuse (longest side) of the right triangle.\\\end{minipage}}`

Therefore:

`\begin{aligned}DE^2+EF^2&=DF^2\\64^2+EF^2&=81.7^2\\EF^2&=81.7^2-64^2\\EF&=√(81.7^2-64^2)\\EF&=√(2578.89)\\EF&=50.7827726...\\EF&=50.8\; \sf units\;(nearest\;tenth)\end{aligned}`

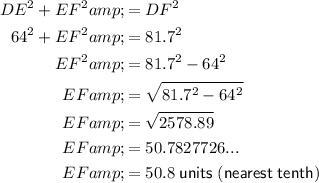
To find the angles D and F, use the Law of Sines.

`\boxed{\begin{minipage}{7.6 cm}\underline{Law of Sines} \\\\$(\sin A)/(a)=(\sin B)/(b)=(\sin C)/(c) $\\\\\\where:\\ \phantom{ww}$\bullet$ $A, B$ and $C$ are the angles. \\ \phantom{ww}$\bullet$ $a, b$ and $c$ are the sides opposite the angles.\\\end{minipage}}`

For triangle DEF:

`(\sin D)/(EF)=(\sin E)/(DF)=(\sin F)/(DE)`

Substitute the known exact values into the equation:

`(\sin D)/(√(2578.89))=(\sin 90^(\circ))/(81.7)=(\sin F)/(64)`

`(\sin D)/(√(2578.89))=(1)/(81.7)=(\sin F)/(64)`

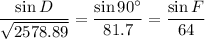
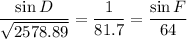
Solve for angle D:

`\begin{aligned}(\sin D)/(√(2578.89))&=(1)/(81.7)\\\\\sin D&=(√(2578.89))/(81.7)\\\\D&=\sin^(-1)\left((√(2578.89))/(81.7)\right)\\\\D&=38.4313259...\\\\D&=38.4^(\circ)\;\sf (nearest\;tenth)\end{aligned}`

Solve for angle F:

`\begin{aligned}(\sin F)/(64)&=(1)/(81.7)\\\\\sin F&=(64)/(81.7)\\\\F&=\sin^(-1)\left((64)/(81.7)\right)\\\\F&=51.5686740...\\\\F&=51.6^(\circ)\;\sf (nearest\;tenth)\end{aligned}`

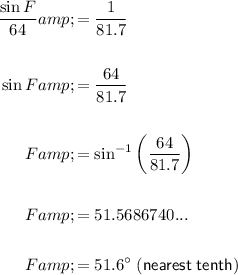
Therefore:

• D = 38.4°
• E = 90°
• F = 51.6°
• DE = 64 units
• EF = 50.8 units
• DF = 81.7 units