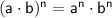Answer:
Third one:
![\sf 5 x^2y^3 \sqrt[3]{x^2}](https://img.qammunity.org/2024/formulas/mathematics/college/hk6vy23lnf3b804etyulm53noiwn76m5s6.png)
Explanation:
Simplify the expression:
![\sf 5 \sqrt[3]{x} \cdot x^{(7)/(3)} \cdot y^{(7)/(4)} \cdot \sqrt[4]{y^5}](https://img.qammunity.org/2024/formulas/mathematics/college/o3wv212pqkield74fh632w014r7i429tx1.png)
Convert cube root in terms of power.
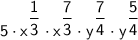
Simplify the expression using the product of powers rule.
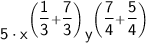
Simplify the expression of power.
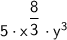
Convert the power of x in terms of cube root.
![\sf 5\cdot \sqrt[3]{x^8} \cdot y^3](https://img.qammunity.org/2024/formulas/mathematics/college/wc3v1d945tr9j252m7owkky1r92mngltea.png)
Simplify the expression using the cube root rule.
![\sf 5\cdot \sqrt[3]{x^8} \cdot y^3](https://img.qammunity.org/2024/formulas/mathematics/college/wc3v1d945tr9j252m7owkky1r92mngltea.png)
![\sf 5\cdot \sqrt[3]{x^6 \cdot x^2} \cdot y^3](https://img.qammunity.org/2024/formulas/mathematics/college/8a4uh9qgc6nz86lf2lk4d766aq6tbuji7w.png)
![\sf 5\cdot x^2 \cdot \sqrt[3]{x^2} \cdot y^3](https://img.qammunity.org/2024/formulas/mathematics/college/x6ctn0gz4qmvnufhkqtlphlemn41lktx9v.png)
So, the answer is:
![\sf 5 x^2y^3 \sqrt[3]{x^2}](https://img.qammunity.org/2024/formulas/mathematics/college/hk6vy23lnf3b804etyulm53noiwn76m5s6.png)

Note:
Power rule:
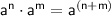
Product rule: