Question

A ship sails 35 km on a bearing of 042°. a) How far north has it travelled? b) How far east has it travelled? •​

Answer 1

a) The ship has traveled approximately 23.42 km north.

b) The ship has traveled approximately 26.01 km east.

Explanation:

let,

• AB is north distance.
• OB is East distance.
• The bearing angle is ∡O = 42°.

While joining the point it makes a right-angled triangle.

So, with respect to ∡O= 42°

• Opposite = AB
• Adjacent = OB
• So, Hypotenuse = AO =35 km

Let's find the distance:

a) North Distance (AB):

You can use the sine function to find AB because AB is opposite to angle ∡O.

`\sf Sin (Angle) = (Opposite)/(Hypotenuse)=(AB)/(AO)`

Substituting value

`\sf Sin(042) =(AB)/(35)`

Doing crisscross multiplication:

`\sf AB = 35 * sin(042)`

`\sf AB = 23. 42 \textsf{ in nearest term}`

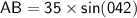
So, the ship travels approximately 23.42 km north.

`\hrulefill`

b) East Distance (OB):

You can use the cosine function because OB is adjacent to angle ∡O.

`\sf Cos (Angle) = (Adjacent)/(Hypotenuse) = (OB)/(AO)`

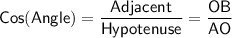
Substituting value

`\sf Cos(042) =(OB)/(35)`

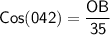
Doing crisscross multiplication:

`\sf OB = 35 * cos(042)`

`\sf OB = 26.01 \textsf{ in nearest term}`

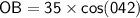
So, the ship travels approximately 26.01 km east.