Question

Let f be the piecewise function given above. The value of ∫80f(x)ⅆx is

Answer 1

The value of the integral from 0 to 8 of the function
`\( f(x) \)` is 2. This corresponds to option (A).

To calculate the value of the integral of the piecewise function
`\( f(x) \)` from 0 to 8, we break the integral into three parts according to the function's definition:

The value of the integral of the piecewise function \( f(x) \) from 0 to 8 is 2, which corresponds to option (A).

The piecewise function
`\( f(x) \)` is defined as 2 for
`\( 0 \leq x < 2 \)`, 3 for
`\( 2 \leq x < 3 \)`, and -1 for
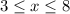`\( 3 \leq x \leq 8 \)`. To find the integral of
`\( f(x) \)` over the interval from 0 to 8, we evaluate the integral over each segment defined by the piecewise function and then sum these values.

Detailed Explanation:

Step 1: Divide the Integral

We divide the integral into three segments according to the definition of
`\( f(x) \)`:

`\[ \int_(0)^(8) f(x) dx = \int_(0)^(2) 2 dx + \int_(2)^(3) 3 dx + \int_(3)^(8) (-1) dx \]`

### Step 2: Compute Each Integral Separately

The integrals of constant functions over an interval are computed as the product of the constant and the interval length:

1.
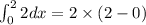
`\( \int_(0)^(2) 2 dx = 2 * (2 - 0) \)`

2.
`\( \int_(2)^(3) 3 dx = 3 * (3 - 2) \)`

3.
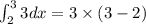
`\( \int_(3)^(8) (-1) dx = -1 * (8 - 3) \)`

Step 3: Evaluate Each Integral

- For
`\( 0 \leq x < 2 \)`:
`\( \int_(0)^(2) 2 dx = 4 \)`

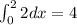
- For
`\( 2 \leq x < 3 \)`:
`\( \int_(2)^(3) 3 dx = 3 \)`

- For
`\( 3 \leq x \leq 8 \)`:
`\( \int_(3)^(8) (-1) dx = -5 \)`

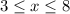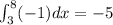
Step 4: Add the Results

We add the results of each segment to find the total integral:

`\[ 4 + 3 - 5 = 2 \]`

Thus, the value of the integral from 0 to 8 of the function
`\( f(x) \)` is 2.

the complete Question is given below:

Answer 2

The value of the definite integral, we need to evaluate the integral for each piecewise function over its corresponding interval and then sum up the results. The value of the integral of the function f(x) over the interval [0, 8] is 2.

The value of the definite integral
`$\int_0^8 f(x) d x$`,

we need to evaluate the integral for each piecewise function over its corresponding interval and then sum up the results. The function f(x) is defined in three different intervals:
1. For 0 ≤ x < 2: f(x) = 2
2. For 2 < x < 3: f(x) = 3
3. For 3 ≤ x ≤ 8: f(x) = -1
Let's compute the integral for each interval:
1. Interval [0, 2):

`\int\limits^0_2 {2} \, dx = 4`
2. Interval (2, 3):

`\int\limits^2_3 {3} \, dx = 3`
3. Interval [3, 8]:

`\int\limits^3_8 {-1} \, dx = -5`
Now, sum up the results:
4 + 3 - 5 = 2
So, the value of
`$\int_0^8 f(x) d x$` is 2.