Question

How do i get the area

Answer 1

1. 675.5 cm^2

2. 629.86 cm^2

Explanation:

1. Find the area of the parallelogram first,

Formula for area of parallelogram:

A = B · H, where "B" represents base and "H" represents height.

In this case, B = 15 and H = 14

Plug into formula:

A = B · H

A = 15 · 14

A = 210

Now let's find the area of the trapezoid,

Formula for area of trapezoid:

A =
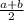`(a + b)/(2)` · H

Where "A" represents one base, "B" represents the other base, and "H" represents the height. When you multiply by 1/2, you just divide everything by 2.

Our given values, A = 15, B = 34, and H = 19.

Plug into formula:

A =
`(a+b)/(2)` · H

A =
`(15 + 34)/(2)` · 19

A = 24.5 · 19

A = 465.5

Now, let's add the area of the parallelogram and the area of the trapezoid together:

210 + 465.5

= 675.5 cm^2

2. Find the area of the two semi-circles, but to make this more simpler, just find the area of one circle using the measurement they give for one semi-circle.

The formula for the area of a semi-circle is the same formula for a full circle except everything is divided by 2-- thus, the name "semi"-circle.

Formula for area of circle:

A = π
`r^(2)`

Where "π" represents pi(3.14 or 22/7) and "r" represents the radius.

Since there is no diameter(two times the radius) or even a radius, we'll have to find it.

Given that the length of the entire figure is 28, we can just divide it by 2 to get the diameter of both semi-circles.

28/2 = 14

The diameter for both semi-circles is 14.

Let's find the radius:

Since the diameter is two times more than the radius, all we have to do is divide the diameter(14) by 2 to get the radius.

14/2 = 7

7 is the radius.

Our values are now 14(radius), π(3.14/22/7), and our exponent of 2 (square).

Now let's plug in our values into the formula:

A = π
`r^(2)`

A = 3.14(7)^2

(^ = to the power of)

Solve exponents first!

A = 3.14(49)

A = 153.86

Now, let's find the rectangle's area,

Formula for area of rectangle:

A = L · W

Where "L" represents length and "W" represents width.

But, we don't have a width! So let's find it out.

Since we know the radius of the semi-circles are 7, all we have to do to find the width of the rectangle is subtract 7 from the total width(24) of the figure. We do this because the radius is the distance from the exact center of a circle to ANY point of the edge of the circle (creds: twinkl). And that means the radius to the top of the semi-circle is 7, so subtract it from the total width.

24 - 7 = 17

17 is the width.

Now let's plug it into our formula:

A = L · W

Our values are, L = 28, and W = 17.

A = 28 · 17

A = 476

Now let's add the area of these two figures together:

153.86 + 476

= 629.86 cm^2