Question

A catapult launches a rock at a castle wall. The rock is launched at a 45° angle with a speed of 22 m/s. The castle wall is 45 m away and is 20 m high. Does the rock make it over the wall?

Answer 1

The rock will hit the wall (assuming that air resistance is negligible and
`g = 9.81\; {\rm m\cdot s^(-2)}`.)

Step-by-step explanation:

In this question, the rock is in a projectile motion. Assuming that air resistance is negligible, the horizontal velocity of the rock would be constant, while the rock would constantly accelerate at
`a_(y) = (-g) = (-9.81)\; {\rm m\cdot s^(-2)}`.

To determine if the rock can make it over the wall, it will be necessary to find the height of the rock when it is at or right above the wall horizontally. This height can be found in the following steps:

• Find the initial horizontal and vertical velocity of the rock.
• Determine the time required for the rock to reach the horizontal position of the wall (assuming that it did not land before reaching there.)
• Make use of the SUVAT equations to find the height of the rock when it is right at or above the wall. The rock would make it over the wall if and only if this height exceeds the height of the wall.

The rock launched at
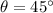`\theta = 45^(\circ)` above the horizon at an initial speed of
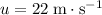`u = 22\; {\rm m\cdot s^(-1)}`. The initial vertical and horizontal velocity components would be:

• Initial horizontal velocity:
  `u_(x) = u\, \cos(\theta)`.
• Initial vertical velocity:
  `u_(y) = u\, \sin(\theta)`.

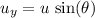Assuming that air resistance on the rock is negligible, the horizontal velocity of the rock would be constant. Divide the horizontal distance from the wall
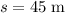`s = 45\; {\rm m}` with this horizontal velocity to find the time required before the rock reaches the wall horizontally (assuming that the rock didn't hit the ground before that.)

`\begin{aligned} t &= (s)/(u_(x)) \\ &= (s)/(u\, \cos(\theta)) \\ &= (45)/(22\, \cos(45^(\circ)))\; {\rm m\cdot s^(-1)} \\ &\approx (45)/(11√(2))\; {\rm m\cdot s^(-1)}\end{aligned}`.

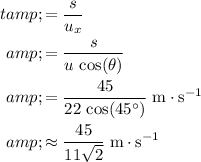Apply the SUVAT equation
`x_(y) = (1/2)\, a_(y)\, t^(2) + u_(y)\, t` to find the vertical displacement (height) of the rock when it is right at (or above) the wall:

`\begin{aligned}x_(y) &= (1)/(2)\, (-g)\, \left((s)/(u\, \cos(\theta))\right)^(2) + u\, \sin(\theta)\, t \\ &= (1)/(2)\, (-9.81)\, \left((45)/(11√(2))\right)^(2) + \left((22)\, \cos(45^(\circ))\right)\, \left((45)/(11√(2))\right) \\ &\approx 3.96\; {\rm m}\end{aligned}`.

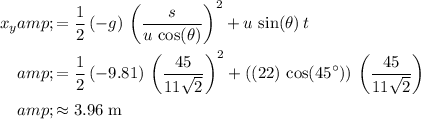In other words, the height of the rock would be approximately
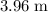`3.96\; {\rm m}` when it is right at the position of the wall. Since this height is less than the height of the wall, the rock would hit the wall instead of flying over the wall.