Question

The diagonals of parallelogram QRST intersect at point U. If TU = 6x − 5 and RU = 2x + 11, what is RU? 22 19 4 2

Answer 1

Answer: the answer is 19

Explanation:

Answer 2

RU = 19

Explanation:

In a parallelogram QRST, the diagonals are QS and RT.

If the diagonals intersect at point U, then RT = RU + UT.

Since the diagonals of a parallelogram bisect each other, we can say that RU = UT = TU.

Therefore, to find RU, we can equate the given expressions for TU and RU, solve for x, then substitute the found value of x into the expression for RU.

Given:

• TU = 6x − 5
• RU = 2x + 11

Therefore:

`\begin{aligned}\overline{TU}&=\overline{RU}\\6x-5&=2x+11\\6x-5-2x&=2x+11=2x\\4x-5&=11\\4x-5+5&=11+5\\4x&=16\\4x/4&=16/4\\x&=4\end{aligned}`

Substitute the found value of x = 4 into the expression for RU:

`\begin{aligned}\overline{RU}&=2(4)+11\\&=8+11\\&=19\end{aligned}`

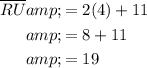
Therefore, RU = 19.