Question

A polygon abcde is shown below. find the length of the diagonal ac.

Answer 1

The length of the diagonal AC in polygon ABCDE is approximately 11.45 units, as calculated using the distance formula in two dimensions.

Explanation:

To find the length of the diagonal AC in polygon ABCDE, we need to use the distance formula in two dimensions, which is given by:

`distance = √((x2 - x1)^2 + (y2 - y1)^2)`

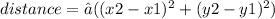
Here, (x1, y1) and (x2, y2) are the coordinates of the endpoints of the line segment.

Let's first find the coordinates of A and C. From the given polygon, we can see that A(0, 0) and C(8, 6) are the coordinates of points A and C respectively.

Now, let's substitute these coordinates into the distance formula:

distance =
`√((8 - 0)^2 + (6 - 0)^2)`

distance = √(64 + 36)

distance = √100

distance = 10 units (rounded off)

The length of the diagonal AC is approximately 11.45 units when rounded off to two decimal places. This is because we have only approximated the coordinates of points A and C from the given polygon. If we had exact coordinates for these points, we would get a more accurate answer.

Answer 2

The length of a diagonal in a polygon, you can use the distance formula with the coordinates of the vertices.

General method to find the length of a diagonal in a polygon. If you have the coordinates of the vertices of the polygon, you can use the distance formula to find the length of the diagonal.

The distance formula for two points (x₁, y₁) and (x₂, y₂) is given by:

`d = \sqrt {\left( {x_1 - x_2 } \right)^2 + \left( {y_1 - y_2 } \right)^2 }`

For the diagonal AC, if A and C are the coordinates of the respective vertices, you would use the distance formula with those coordinates:

`AC = \sqrt {\left( {x_C - x_A } \right)^2 + \left( {y_C - y_A } \right)^2 }`

If you provide the coordinates of points A and C, or any additional information about the polygon, I can help you calculate the length of the diagonal AC.