Answer:
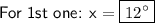

Explanation:
For 1st Question:
Pair of given angles in the picture is vertically opposite angles.
Since,
Vertically opposite angles are two or more angles that are opposite each other at a vertex and are created by two straight intersecting lines.
Vertically opposite angles are equal to each other.
So,
we can write it as:
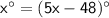
Since both angles have the same measure, the expressions inside the parentheses must be equal.
Therefore:
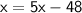
Subtract 5x from both sides:
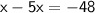
Simplify like terms:

Divide by -4 to isolate x:
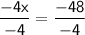
Simplify:
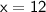
So, value of x is 12°.

For the 2nd Question:
Pair of given angles in the picture is linear pair or angle in a straight line.
Since
A linear pair is a pair of adjacent angles formed by two intersecting lines.
The linear pair of angles are always supplementary as they form on a straight line.
In other words, the sum of two angles in a linear pair is always 180°.
So,
We can write it as:
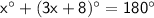
Let's isolate the value of x.
Open Parentheses or bracket:

Simplify like terms:
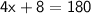
Subtract 8 both sides:
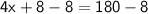
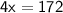
Divide by 4 on both sides:

Simplify:

Therefore, value of x is 43°.