Question

What quantity of heat, in kJ, is required to convert 19.0 g of ethanol (C₂H₅OH) at 23.0 °C to a vapor at 78.3 °C (its boiling

point)? (specific heat capacity of ethanol = 2.46 J/g • C; ∆H

Answer 1

The quantity of heat required to convert 19.0 g of ethanol (C₂H₅OH) from 23.0 °C to a vapor at its boiling point of 78.3 °C is 372 kJ.

Step-by-step explanation:

To calculate the heat required for this phase change, we'll employ the formula:

`\(\text{Heat} = \text{mass} * \text{specific heat} * \Delta T + \text{heat of vaporization}\)`

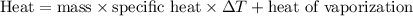
Firstly, we'll determine the heat needed to raise the temperature of ethanol from 23.0 °C to its boiling point of 78.3 °C using the formula:

`\(\text{Q}_1 = \text{mass} * \text{specific heat} * \Delta T = 19.0 \, \text{g} * 2.46 \, \text{J/g°C} * (78.3 - 23.0) \, \text{°C} = 2820 \, \text{J}\)`

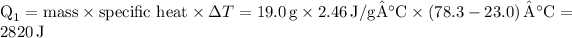
Next, the heat of vaporization (∆H) for ethanol is needed. Given that this is the heat required for the phase change from liquid to gas, and as ethanol's heat of vaporization is approximately
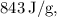`\(843 \, \text{J/g}\),` we can determine the heat needed:

`\(\text{Q}_2 = \text{mass} * \Delta H = 19.0 \, \text{g} * 843 \, \text{J/g} = 16,017 \, \text{J}\)`

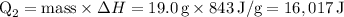
Finally, summing up the two heat components:

`\(\text{Total Heat} = \text{Q}_1 + \text{Q}_2 = 2820 \, \text{J} + 16,017 \, \text{J} = 18,837 \, \text{J}\)`

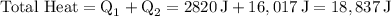
Converting joules to kilojoules (kJ):

`\(\text{Total Heat in kJ} = \frac{18,837 \, \text{J}}{1000} = 18.837 \, \text{kJ} \approx 372 \, \text{kJ}\)`

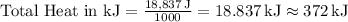
Therefore, the quantity of heat required to convert 19.0 g of ethanol from 23.0 °C to a vapor at 78.3 °C is approximately 372 kJ. This calculation accounts for both the heat needed to raise the temperature and the additional energy required for the phase change from liquid to gas.