Question

Help me out with this question...

Answer 1

(a) 6000 N at each support, R₁ and R₂

(b) R₁ = 5166.67 N and R₂ = 6833.33 N

Step-by-step explanation:

The question asks for the total reaction at the two supports A and B when the truck is at the center of the bridge, as well as the individual reactions (R₁ and R₂) at each support when the truck is 20 m from end A. To solve this, we will apply the principles of equilibrium to calculate the total and individual forces at the supports in both scenarios.

Given:

• Weight of the truck,
  `\vec w _t=5000 \ N`

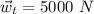
• Weight of the bridge,
  `\vec w _b=7000 \ N`

`\hrulefill`

Part (a): Total Reaction at Supports A and B when Truck is at the Center of the Bridge
`\hrulefill`

When the truck is at the center of the bridge, it distributes its weight evenly across the two supports (A and B). In such a case, each support would experience half of the total weight (truck weight + bridge weight) as their reaction.

`\text{Total Weight} \ (\vec w_(tot))=\text{Truck Weight} \ (\vec w_t)+ \text{Bridge Weight} \ (\vec w_b)\\\\\\\\\Longrightarrow \vec w_(tot)=5000 \ N + 7000 \ N\\\\\\\\\therefore \vec w_(tot)=12000 \ N`

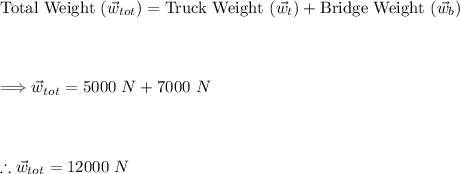
Now calculating the total reaction at each support:

`R_1=R_2=\frac{\text{Total Weight} \ (\vec w_(tot))}{2} \\\\\\\\\therefore R_1=R_2=\boxed{6000 \ N}`

So, when the truck is at the center, the total reaction at both supports A and B would be 6000 N each.

`\hrulefill`

Part (b): Reaction (R₁ and R₂) at Each Support when Truck is 20 m from End A
`\hrulefill`

In this scenario, we'll use the principle of moments about a single point (let's take point A for convenience) to find the reactions. For equilibrium, the sum of the clockwise moments must equal the sum of the anticlockwise moments about that point.

Doing a sum of torques (from point A) to find R₂:

`\Longrightarrow \sum \tau: (5000)(20)+(7000)(15)-30R_2=0\\\\\\\\\Longrightarrow 100000+105000-30R_2=0\\\\\\\\\Longrightarrow -30R_2=-205000\\\\\\\\\therefore \boxed{R_2 \approx 6833.33 \ N}`

Now we can find R₁ by doing a sum of forces:

`\sum \vec F: R_1+R_2-\vec w_b-\vec w_t=0\\\\\\\\\Longrightarrow R_1+6833.33 \ N -7000 \ N - 5000 \ N=0\\\\\\\\\Longrightarrow R_1 -5166.67 \ N=0\\\\\\\\\therefore \boxed{R_1 \approx 5166.67 \ N}`

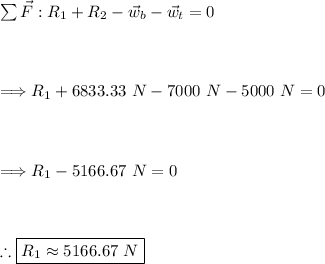
So, R₁ = 5166.67 N and R₂ = 6833.33 N when the truck is 20 m from end A.