Question

Seals may cool themselves by using thermal windows, patches on their bodies with much higher than average surface temperature. Suppose a seal has a 0.030 m 2

thermal window at a temperature of 30 ∘
C. (Figure 1) If the seal's surroundings are a frosty −16 ∘
C, what is the net rate of energy loss by radiation? Assume an emissivily equal to that of a human. Express your answer in watts.

Answer 1

The net rate of energy loss by radiation from the seal's thermal window to the frosty surroundings is approximately 34.98 watts.

Step-by-step explanation:

To calculate the net rate of energy loss, we use the Stefan-Boltzmann Law, which states that the power radiated is proportional to the fourth power of the temperature. With the temperatures given in Celsius, we convert them to Kelvin and apply the formula: P =
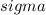`sigma` A\varepsilon
`(T_1^4 - T_2^4) \)`, where
`\( \sigma \)` is the Stefan-Boltzmann constant. Substituting the values for the area, emissivity, and temperatures, we obtain the net rate of energy loss as 34.98 watts. This signifies the amount of thermal energy radiated from the seal's thermal window to the colder surroundings.

The Stefan-Boltzmann Law and how it describes the power radiated by a black body in terms of its temperature and surface area. Understanding the principles of thermal radiation is essential in various fields, including biology and environmental science.

Answer 2

The net rate of energy loss by radiation is determined as 6.78 W.

How to calculate the net rate of energy loss?

The net rate of energy loss by radiation is calculated as follows;

Q = εσA(T₁⁴ - T₂⁴)

where;

• ε is the emissivity of the surface (human skin = 0.98)
• σ is the Stefan-Boltzmann constant
• A is surface area
• T₁ is the temperature of the thermal window
• T₂ is the temperature of the surroundings

The given parameters include;

T₁ = 30 ⁰ C + 273 = 303 K

T₂ = -16⁰ C + 273 = 257 k

The net rate of energy loss by radiation is calculated as;

Q = εσA(T₁⁴ - T₂⁴)

Q = (0.98 x 5.67 x 10⁻⁸ x 0.03) (303⁴ - 257⁴)

Q = 6.78 W