The
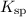 for
for
 is approximately
is approximately
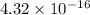 .
.
The solubility product constant
 for a sparingly soluble salt, like
for a sparingly soluble salt, like
 , is the product of the concentrations of its ions raised to the power of their coefficients in the balanced chemical equation.
, is the product of the concentrations of its ions raised to the power of their coefficients in the balanced chemical equation.
The balanced chemical equation for the dissociation of
 is:
is:
![\[ Eu(OH)_2 \rightleftharpoons Eu^(2+) + 2OH^- \]](https://img.qammunity.org/2024/formulas/chemistry/high-school/jypwejknd2peq45wvd81ek4z1ku0dtmlee.png)
The dissociation's equilibrium expression is provided by:
![\[ K_{\text{sp}} = [Eu^(2+)][OH^-]^2 \]](https://img.qammunity.org/2024/formulas/chemistry/high-school/2g1uzys6pm7rtqkpbfxi5apbg46w3y2nlf.png)
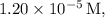
Given that the solubility of
 in a solution of
in a solution of
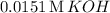 is
is
 , we can use this information to set up the equilibrium concentrations:
, we can use this information to set up the equilibrium concentrations:
![\[ [Eu^(2+)] = 1.20 * 10^(-5) \, \text{M} \]](https://img.qammunity.org/2024/formulas/chemistry/high-school/vpdvc6825tvqjzk4yvjacji3sqkvy8zvd0.png)
![\[ [OH^-] = 2 * [Eu^(2+)] = 2 * 1.20 * 10^(-5) \, \text{M} \]](https://img.qammunity.org/2024/formulas/chemistry/high-school/o5ulhitelh2owfyve5wiz7vdop9elz1dl5.png)
Now, substitute these values into the
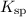 expression:
expression:
![\[ K_{\text{sp}} = (1.20 * 10^(-5)) * (2 * 1.20 * 10^(-5))^2 \]](https://img.qammunity.org/2024/formulas/chemistry/high-school/27isht635r00jgwm4oonppav73mwr6os5x.png)
![\[ K_{\text{sp}} = 1.20 * 10^(-5) * 4 * (1.20 * 10^(-5))^2 \]](https://img.qammunity.org/2024/formulas/chemistry/high-school/v6afi6r7catov504dsp6782ifczofvvbb2.png)
![\[ K_{\text{sp}} = 4.32 * 10^(-16) \]](https://img.qammunity.org/2024/formulas/chemistry/high-school/nkmnfw9sb9cvronv311usn5gp24s95n6c8.png)
Therefore, the
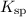 for
for
 is approximately
is approximately
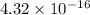 .
.