The closest option is:
![\[1.583 \, \text{m/s}; \, 8^\circ\]](https://img.qammunity.org/2024/formulas/physics/high-school/4k9ha3ffyd62w1ql22cdxk16i6lqll1i7t.png)
To find the true speed and direction of the golf ball, you can use vector addition. The components of the velocity vectors can be calculated using trigonometric functions.
Let's break down the initial velocity of the golf ball into its horizontal and vertical components:
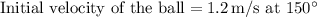
Horizontal component
 :
:
![\[ V_{\text{h,1}} = 1.2 \, \text{m/s} * \cos(150^\circ) \]](https://img.qammunity.org/2024/formulas/physics/high-school/uyo46kuih25ikyqolz6fpai5ux21534xac.png)
Vertical component
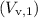 :
:
![\[ V_{\text{v,1}} = 1.2 \, \text{m/s} * \sin(150^\circ) \]](https://img.qammunity.org/2024/formulas/physics/high-school/jnx50kntwg3v593wb063xf19an34ramvb5.png)
Now, let's break down the wind velocity into its horizontal and vertical components:
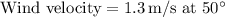
Horizontal component
 :
:
![\[ V_{\text{h,w}} = 1.3 \, \text{m/s} * \cos(50^\circ) \]](https://img.qammunity.org/2024/formulas/physics/high-school/61nh99eo05xhxfcksr659omgy6uznb2c3v.png)
Vertical component
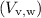 :
:
![\[ V_{\text{v,w}} = 1.3 \, \text{m/s} * \sin(50^\circ) \]](https://img.qammunity.org/2024/formulas/physics/high-school/dnz2g008q4lzxrxcov3jnsnuaw1cqi85fm.png)
Now, add the corresponding components:
![\[ V_{\text{h,total}} = V_{\text{h,1}} + V_{\text{h,w}} \]](https://img.qammunity.org/2024/formulas/physics/high-school/nqdjbu5ypppgf4efjmud8cxubvpyd8r0bb.png)
![\[ V_{\text{v,total}} = V_{\text{v,1}} + V_{\text{v,w}} \]](https://img.qammunity.org/2024/formulas/physics/high-school/7rcx822dds6vtgu0hhan8j3obvn668qjh0.png)
The true speed
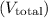 is given by the magnitude of the total velocity vector:
is given by the magnitude of the total velocity vector:
![\[ V_{\text{total}} = \sqrt{V_{\text{h,total}}^2 + V_{\text{v,total}}^2} \]](https://img.qammunity.org/2024/formulas/physics/high-school/vzpw5nnprva9g5abzdtct35a98255ru9fd.png)
The direction
 is given by the arctangent of the ratio of the vertical and horizontal components:
is given by the arctangent of the ratio of the vertical and horizontal components:
![\[ \theta_{\text{total}} = \tan^(-1)\left(\frac{V_{\text{v,total}}}{V_{\text{h,total}}}\right) \]](https://img.qammunity.org/2024/formulas/physics/high-school/bbg6tvybswj2ir5mieak3mo6mhqg5n6wt6.png)
Now, let's calculate these values and compare them to the given options.
![\[ V_{\text{h,total}} \approx 1.583 \, \text{m/s} \]](https://img.qammunity.org/2024/formulas/physics/high-school/8ppw0w11f2ej6cmqj0q7hibwm8ch2hg3wp.png)
![\[ V_{\text{v,total}} \approx 0.166 \, \text{m/s} \]](https://img.qammunity.org/2024/formulas/physics/high-school/menly839yb3zxgzdcr2jh7s02f6zobxn7b.png)
![\[ V_{\text{total}} \approx √(1.583^2 + 0.166^2) \approx 1.593 \, \text{m/s} \]](https://img.qammunity.org/2024/formulas/physics/high-school/9pd1crega8aro8roto1igfiw258fh61ohf.png)
![\[ \theta_{\text{total}} \approx \tan^(-1)\left((0.166)/(1.583)\right) \approx 6.010^\circ \]](https://img.qammunity.org/2024/formulas/physics/high-school/pq0jmx17s3c9x6rfjux6lx814ad3qk9y0j.png)
So, the closest option is:
![\[1.583 \, \text{m/s}; \, 8^\circ\]](https://img.qammunity.org/2024/formulas/physics/high-school/4k9ha3ffyd62w1ql22cdxk16i6lqll1i7t.png)