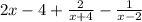The correct choice is D.
To find the partial fraction decomposition of the given rational function
 , we first factor the denominator.
, we first factor the denominator.
The denominator factors as follows:
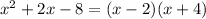
Now, we can express the given rational function as a sum of partial fractions with undetermined coefficients:
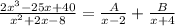
where A and B are constants.
Next, we clear the fractions by multiplying both sides by the common denominator (x−2)(x+4):

Now, we can determine the values of A and B by comparing coefficients. We can do this by substituting appropriate values for x that eliminate one of the terms, making it easier to solve for the unknowns.
Let's start with x=2:
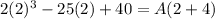
Simplifying the left side:
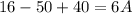
which gives A=−1.
Now, let's try x=−4:

Simplifying the left side:
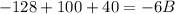
which gives B=−12.
Now we can write the original expression as partial fractions:
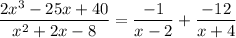
To write this in the form given in the choices, factor out the common factor from the numerators:
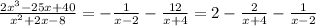
Now, compare this to the provided choices:
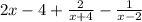
Complete Question:
What is the quotient and remainder, written as partial fractions, of
 ?
?
a.
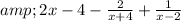
b.
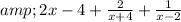
c.

d.