Question

Consider the polynomials p(x) = 9x + 2x^2 and q(x)=−9. Find the x-coordinate(s) of the point(s) of intersection of these two polynomials. What is the sum of these x-coordinates?

Answer 1

`-(9)/(2)`

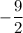
Explanation:

To find the x-coordinate(s) of the point(s) of intersection of the two polynomials p(x) and q(x), we need to set the two polynomials equal to each other and solve for x.

`\begin{aligned}p(x)&=q(x)\\9x + 2x^2 &= -9\end{aligned}`

Rearrange the equation to put it in standard quadratic form, ax² + bx + c = 0:

`\begin{aligned}9x + 2x^2 +9&= -9+9\\9x + 2x^2 +9&=0\\ 2x^2 +9x +9&=0\\\end{aligned}`

Now, solve for x using the quadratic formula.

`\boxed{\begin{array}{c}\underline{\sf Quadratic \;Formula}\\\\x=(-b \pm √(b^2-4ac))/(2a)\\\\\textsf{when}\;ax^2+bx+c=0\\\\\end{array}}`

For this equation:

• a = 2
• b = 9
• c = 9

Substitute these values into the quadratic formula:

`x = (-9 \pm √(9^2 - 4 \cdot 2 \cdot 9))/(2 \cdot 2)`

`x = (-9 \pm √(81 - 72))/(4)`

`x = (-9 \pm √(9))/(4)`

`x = (-9 \pm 3)/(4)`

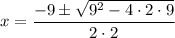
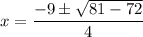
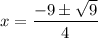
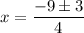
So the two possible x-coordinates of the points of intersection are:

`x_1 = (-9 + 3)/(4) = (-6)/(4) = -(3)/(2)`

`x_2 = (-9 - 3)/(4) = (-12)/(4) = -3`

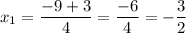
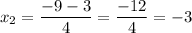
The sum of these x-coordinates is:

`-(3)/(2) +(- 3) = -(3)/(2)-(6)/(2) =(-3-6)/(2)= -(9)/(2)`

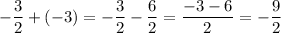
Therefore, the sum of the x-coordinates of the points of intersection of polynomials p(x) and q(x) is:

`\large\boxed{\boxed{-(9)/(2)}}`