Question

Do 9 and 11 and explain u get 100 points

Answer 1

9) GD = 222

10) DF = 140

Explanation:

Question 9

The diagram shows line GD, where G and D are the endpoints, and points F and E are on the line.

Given lengths:

• FE = 37
• FD = 3x + 194
• GD = x + 241
• GE = x + 141

To find the expression for ED, subtract FE from FD:

`\begin{aligned}ED&=FD-FE\\ED&=3x+194-37\\ED&=3x+157\end{aligned}`

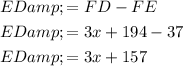
We know that the sum of the smaller segments should be equal to the length of the larger segment. In this case, the sum of GE and ED should be equal to GD:

`\begin{aligned}GE+ED&=GD\\x+141+3x+157&=x+241\\4x+298&=x+241\\4x+298-x&=x+241-x\\3x+298&=241\\3x+298-298&=241-298\\3x&=-57\\3x/3&=-57/3\\x&=-19\end{aligned}`

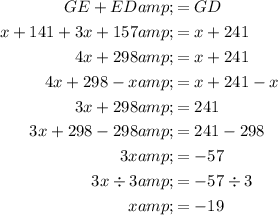
To find the length of GD, we can substitute the found value of x into the expression for GD:

`\begin{aligned}GD&=x+214\\GD&=-19+241\\GD&=222\end{aligned}`

Therefore, the length of GD is 222.

`\hrulefill`

Question 11

The diagram shows line DG, where D and G are the endpoints, and points E and F are on the line.

Given lengths:

• EF = 13x - 155
• DG = x + 204
• DF = 6x + 32
• EG = 161

To find the expression for DE, subtract EF from DF:

`\begin{aligned}DE&=DF-EF\\DE&=(6x+32)-(13x-155)\\DE&=6x+32-13x+155\\DE&=187-7x\end{aligned}`

We know that the sum of the smaller segments should be equal to the length of the larger segment. In this case, the sum of DE and EG should be equal to DG:

`\begin{aligned}DE+EG&=DG\\187-7x+161&=x+204\\348-7x&=x+204\\348-7x-x&=x+204-x\\348-8x&=204\\348-8x-348&=204-348\\-8x&=-144\\-8x / -8&=-144/-8\\x&=18\end{aligned}`

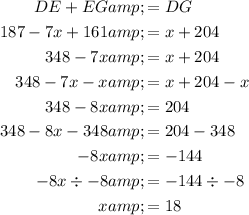
To find the length of DF, we can substitute the found value of x into the expression for DF:

`\begin{aligned}DF&=6(18)+32\\DF&=108+32\\DF&=140\end{aligned}`

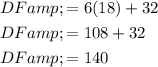
Therefore, the length of DF is 140.

Answer 2

9) GD = 222

11)DF = 140.

Explanation:

For question 9:

Given:

• GD= x+241
• FE = 32
• ED = 3x+194
• GE = x+141

Since GD is a straight line and F and E are the points in GD.

We have;

GE = GF+FE

Substituting value

x+141 = GF + 37

GF = x+141 -37

GF = x + 104 ........[i]

Here,

GF = GD - FD

Substituting value

GF = x+241 - (3x+194)

GF = x+241 - 3x-194)

Similarly:

GF = -2x +47

Substituting value in equation i.

-2x+47 = x+104

Adding 2x and subtracting 104 on both sides

-2x+2x+47-104 = x+2x+104-104

-57 = 3x

Dividing both sides by 3.

`\sf x = (-57)/(3)`

x= -19.

Now,

GD = x+241 = -19+241 =222

Therefore, GD = 222.

`\dotfill`

Question no. 11

Given:

• DG = x+204
• EF = 13x -155
• DF = 6x + 32
• EG = 161

Since DG is a straight line and E and F are the points in DG..

We get:

DG = DE + EG

Substituting value:

x+204 = DE + 161

Subtracting both sides by 161.

x+204-161 = DE

DE = x+43......[i]

Similarly:

DE = DF - EF

Substituting value:

x+43 = 6x+32 -(13x -155)

x + 43 = 6x + 32 -13x + 155

Simplifying like terms

x+43 = -7x + 187

Adding 7x and subtracting 43 on both sides

x+43+7x -43 = -7x + 187+7x -43

8x = 144

Dividing both sides by 8.

`\sf (8x)/(8) = (144)/(8)`

x = 18.

Now,

`\sf DF = 6x + 32 =6 * 18 + 32 =140.`

Therefore, DF = 140.