Answer:
Explanation:
The average rate of change is the slope. Slope has a formula that is the change in y over the change in x, which is a fraction. The only time a fraction can have a vlue of 0 is where the numerator of the fraction is equal to 0 (since we are not allowed to have a denominator of 0). If the change in y is in the top of the slope fraction, then we have to find the interval where the y values are the same. I'll show you one where the y values are not the same so you can compare it to the slope where the y values are the same. We will find the slope of choice A.
When x = -3, y = 0 so the coordinate is (-3, 0).
When x = 5, y = 5 so the coordinate is (5,4). Now let's find the slope (aka average rate of change) between those 2 coordinates:
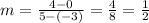 and the top of the fraction is a 1, not a 0, so the average rate of change between these 2 points is 1/2, not 0. Now let's do D.
and the top of the fraction is a 1, not a 0, so the average rate of change between these 2 points is 1/2, not 0. Now let's do D.
When x = -3, y = 0 so the coordinate is (-3, 0).
When x = -1, y = 0 so the coordinate is (-1, 0). The slope between these 2 points is
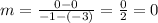 This fraction is equal to 0 because the numerator is 0. Choice D is the one you want.
This fraction is equal to 0 because the numerator is 0. Choice D is the one you want.