Question

Your friend hikes six miles west and 3 miles north. You hike to the same location, but take a different trail that is

a direct path. How far do you hike?

Answer 1

If you take a direct path to the same location, you would hike approximately 6.708 miles.

Explanation:

Your friend's hike follows a path that involves moving 6 miles west and then 3 miles north. This forms a right-angled triangle.

Using the Pythagorean theorem (a² + b² = c²) where 'a' and 'b' are the lengths of the sides of the triangle and 'c' is the length of the hypotenuse (direct path you take):

a = 6 miles (west)

b = 3 miles (north)

c² = a² + b²

c² = 6² + 3²

c² = 36 + 9

c² = 45

Taking the square root of both sides:

c = √45 ≈ 6.708

So, if you take a different trail and follow a direct path, you would hike approximately 6.708 miles to the same location.

Answer 2

`\textsf{ I would hike 6.71 miles or 3 $ \sf √(5) $ miles }`

Explanation:

I and my friend are forming a right-angled triangle where one side is 6 miles and the other side is 3 miles, with my friend's route going west and north.

I am taking the hypotenuse, which is the direct path between the two points.

Using the Pythagorean theorem, which states that in a right triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides:

`\sf c^2 = a^2+ b^2`

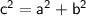
Where:

• c is the direct distance you hike.
• a is the distance your friend hiked west (6 miles).
• b is the distance your friend hiked north (3 miles).

Plugging in these values:

`\sf \begin{aligned}\sf c^2&\sf = 6^2+ 3^2\\\\&\sf = 36 + 9\\\\&\sf = 45 \end{aligned}`

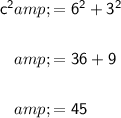
Taking the square root of both sides to find c:

`\begin{aligned} \sf c & \sf = √(45)\\\\&\sf = √((9 * 5))\\\\&\sf = 3√(5) \textsf{ miles }\\\\\sf c &\sf \approx 6.71 \textsf{ miles in 2. d. p}\end{aligned}`

`\textsf{ I would hike 6.71 miles or 3 $ \sf √(5) $ miles }`