Question

A physics instructor wants to produce a double-slit interference pattern large enough for her class to see. For the size of the room, she decides that the distance between successive bright fringes on the screen should be at least 2.30 cm.

If the slits have a separation d=0.0200 mm, what is the minimum distance from the slits to the screen when 632.8 nm light from a He-Ne light is used?

Answer 1

Approximately
`0.727\; {\rm m}`.

Step-by-step explanation:

For a particular fringe in a double-slit interference experiment, the following ratio approximately holds:

`\displaystyle (n\, \lambda)/(d) \approx (x)/(L)`,

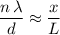Where:

• 
  `n\, \lambda` is the path difference (between the slits) that results in the given fringe,
• 
  `d` is the distance between the two slits,
• 
  `x` is the distance between the given fringe and the central maximum, and
• 
  `L` is the distance between the slits and the screen.

In this question, the distance
`L` between the slit and the screen can be found in the following steps:

• Derive the path difference
  `n\, \lambda` required to produce the first bright fringe.
• Apply unit conversion and ensure that all quantities are measured in standard units.
• Rearrange the ratio to find distance
  `L` between the screen and the slits.

To produce a bright fringe on the screen, the path difference
`n\, \lambda` between the slits needs to be an integer multiple of the wavelength
`\lambda`. In other words,
`n` needs to be an integer. For example:

• 
  `n = 0` produces the bright fringe at the central line.
• 
  `n = 1` produces the first pair of bright fringes around the central line.

For the fringes near the central line, the distance between the two slits is much greater than the path differences that produced the fringes. As a result, the distance between consecutive fringes are approximately the same. Hence, to ensure a minimum distance between each successive pairs of bright fringes, it would be approximately sufficient to ensure that distance between the central line and the first pair of fringes (where
`n = 1`.)

Apply unit conversion and ensure that all distances and wavelengths are measured in the standard unit of meters:

Wavelength:

`\begin{aligned} \lambda &= 632.8\; {\rm nm} \\ &= (623.8\; {\rm nm}) * \frac{1\; {\rm m}}{10^(9)\; {\rm nm}} \\ &= 6.328* 10^(-7)\; {\rm m} \end{aligned}`.

Distance between the two slits:

`\begin{aligned} d &= 0.0200\; {\rm mm} \\ &= (0.0200\; {\rm mm}) * \frac{1\; {\rm m}}{10^(3)\; {\rm mm}} \\ &= 2.0 * 10^(-5)\; {\rm m} \end{aligned}`.

Minimum distance between the first pair of bright fringes and the central line:

`\begin{aligned}x &= (2.30\; {\rm cm}) * \frac{1\; {\rm m}}{10^(2)\; {\rm cm}} \\ &= 2.30 * 10^(-2)\; {\rm m}\end{aligned}`.

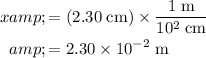Rearrange the equation between the two ratios to approximate
`L`, the distance between the slits and the screen:

`\begin{aligned} L &\approx (x\, d)/(n\, \lambda) \\ &= ((2.30 * 10^(-2))\, (2.00* 10^(-5)))/((1)\, (6.328 * 10^(-7))) \; {\rm m}\\ &\approx 0.727\; {\rm m} \end{aligned}`.

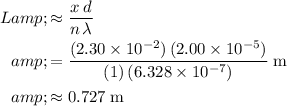Therefore, a minimum distance of approximately
`0.727\; {\rm m}` would be sufficient for ensuring the minimum distance between the first few adjacent bright fringes.