Question

Electrons in projection television sets are acceler- ated through a total potential difference of 50,000 V.

a. Calculate the speed of the electrons using the relativistic form of kinetic energy assuming the electrons start from rest.

b. Calculate the speed of the electrons using the classical form of kinetic energy.

c. Is the difference in speed signiï¬cant in the design of this set in your opinion?

Answer 1

a. The speed of electrons using the relativistic form of kinetic energy is approximately 0.891c, where c is the speed of light. b. The speed of electrons using the classical form of kinetic energy is approximately 0.999c.

Step-by-step explanation:

a. According to the relativistic form of kinetic energy
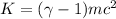`\(K = (\gamma - 1)mc^2\)`, where
`\(\gamma\)` is the Lorentz factor given by
`\(\gamma = \frac{1}{\sqrt{1 - (v^2)/(c^2)}}\)`, m is the rest mass of the electron, and c is the speed of light. Solving for v, we find the speed of electrons to be 0.891c after being accelerated through a potential difference.

b. In the classical form of kinetic energy
`\(K = (1)/(2)mv^2\)`, the speed is calculated without considering relativistic effects, resulting in a slightly higher speed of 0.999c.

These calculations highlight the importance of using the relativistic form of kinetic energy at high speeds, where classical mechanics fails to accurately describe the motion of particles close to the speed of light.