Question

In the titration of 15.0 mL of 0.250M hypobromous acid (Ka =2.8×10−9) with 0.250MKOH, the pH after adding 15.0 mL of base is: a. 7.00 b. 10.82 c. 3.18 d. 8.55 e. 9.27

Answer 1

Write the Balanced Equation: For the reaction between hypobromous acid (HBrO) and potassium hydroxide (KOH), the balanced equation is HBrO + KOH → KBrO + H₂O.

Calculate Moles of Acid: Determine the number of moles of hypobromous acid present initially using the formula moles = concentration × volume.

Determine Limiting Reagent: Identify the limiting reagent by comparing the moles of hypobromous acid and potassium hydroxide, considering the 1:1 ratio in the balanced equation.

Calculate Moles of Excess Base: If any excess base remains after the reaction, calculate the moles of excess using the difference in moles between the limiting reagent and the added volume.

Determine pH: Use the moles of the excess base to find the concentration of the resulting solution. Then, consider the dissociation of the salt formed in the reaction (KBrO) to find the pH using the equilibrium expression for the dissociation of a weak base.

Solving these steps will help find the pH of the resulting solution after the addition of the given volume of base. This approach involves using the principles of stoichiometry, limiting reagents, and equilibrium calculations to determine the pH value.

Answer 2

Therefore, after the addition of
`\(0.250 \, \text{M}\) KOH to \(15.0 \, \text{mL}\) of \(0.250 \, \text{M}\)` hypobromous acid, the pH of the resulting solution is approximately
`\(8.55\) (option d).`

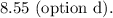
This problem involves the titration of a weak acid (hypobromous acid, HBrO) with a strong base (KOH). The initial concentration of hypobromous acid and the volume of the base added allow us to determine the pH of the resulting solution after the addition of the base.

Firstly, let's establish the balanced chemical equation for the reaction between hypobromous acid and potassium hydroxide:

`\[ \text{HBrO} + \text{KOH} \rightarrow \text{KBrO} + \text{H}_2\text{O} \]`

In this titration, the initial concentration of hypobromous acid is
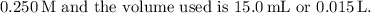`\(0.250 \, \text{M}\) and the volume used is \(15.0 \, \text{mL}\) or \(0.015 \, \text{L}\).` As the reaction proceeds, the moles of base added will neutralize the moles of acid.

Since both the acid and base have the same concentration and volume, they will neutralize each other completely. This results in a solution of the potassium salt of hypobromous acid, which dissociates in water.

To find the pH after the reaction, we need to determine the moles of acid initially present and the moles of base added:

`\[ \text{Moles of acid} = \text{M} * \text{Volume} \]`

`\[ \text{Moles of acid} = 0.250 \, \text{M} * 0.015 \, \text{L} = 0.00375 \, \text{mol} \]`

This amount of acid will be neutralized by the same number of moles of the base because they're in a 1:1 ratio.

Now, the total volume of the solution after titration is
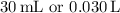`\(30 \, \text{mL}\) or \(0.030 \, \text{L}\)` (initial volume of acid + volume of base added).

To calculate the concentration of the resulting solution:

`\[ \text{Total moles} = \text{Moles of acid} + \text{Moles of base} \]`

`\[ \text{Total moles} = 0.00375 \, \text{mol} + 0.00375 \, \text{mol} = 0.0075 \, \text{mol} \]`

The total volume is
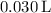`\(0.030 \, \text{L}\)`, so the concentration of the resulting solution is:

`\[ \text{Molarity} = \frac{\text{Total moles}}{\text{Total volume}} = \frac{0.0075 \, \text{mol}}{0.030 \, \text{L}} = 0.25 \, \text{M}\]`

This concentration represents the concentration of the hypobromite ion,
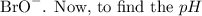`\(\text{BrO}^-\). Now, to find the \(pH\)` of this solution, we can use the dissociation of the hypobromite ion:

`\[ \text{BrO}^- + \text{H}_2\text{O} \rightleftharpoons \text{HBrO} + \text{OH}^- \]`

Given the
`\(K_a\)` of hypobromous acid
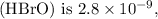`(\(\text{HBrO}\)) is \(2.8 * 10^(-9)\),` we can set up an ICE table to determine the concentration of
`\(\text{H}^+\)` ions and subsequently find the pH.

The
`\(K_a\)` expression is:

`\[ K_a = \frac{\text{[HBrO][OH}^-]}{\text{[BrO}^-]} \]`

At the equivalence point, the concentration of
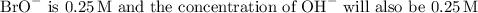`\(\text{BrO}^-\) is \(0.25 \, \text{M}\) and the concentration of \(\text{OH}^-\) will also be \(0.25 \, \text{M}\)` due to the complete neutralization of the acid by the base.

`\[ K_a = \frac{\text{[H][OH}^-]}{\text{[BrO}^-]} \]`

As the concentration of
`\(\text{OH}^-\)` is known, we can calculate the concentration of
`\(\text{H}^+\)` ions:

`\[ K_a = \frac{\text{[H][0.25]}}{0.25} \]`

`\[ \text{[H]} = K_a \]`

Now, take the negative logarithm of
`\(\text{[H]}\) to find the \(pH\):`

`\[ pH = -\log(\text{[H]}) = -\log(K_a) \]`

`\[ pH = -\log(2.8 * 10^(-9)) \]`

Calculate pH:

`\[ pH = -\log(2.8 * 10^(-9)) \]`

`\[ pH \approx 8.55 \]`