Question

a planet follows an elliptical path described by 16x^(2)+4y^(2)=64. a comet follows the parabolic path y=x^(2)-4. where might the comet intersec the orbiting planet?

Answer 1

The comet intersects the orbiting planet at the points (2,0) and (−2,0).

To find the intersection points of the elliptical path and the parabolic path, we need to solve the system of equations formed by the given equations.

The equations are:

Elliptical path:
`16 x^2+4 y^2=64`

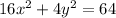
Parabolic path:
`y=x^2-4`

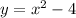
Substitute the expression for y from the parabolic path into the equation for the elliptical path:

`16 x^2+4\left(x^2-4\right)^2=64`

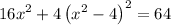
Now, simplify and solve for x:

`\begin{aligned}& 16 x^2+4\left(x^4-8 x^2+16\right)=64 \\& 16 x^2+4 x^4-32 x^2+64=64 \\& 4 x^4-16 x^2+64=0\end{aligned}`

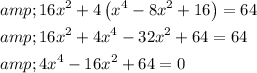
Now, let's factor the quadratic in terms of
`x^2`.

`4\left(x^2-4\right)^2=0`

This quadratic equation has solutions when
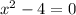`x^2-4=0`. Solve for x:

`\begin{aligned}& x^2-4=0 \\& x^2=4 \\& x= \pm 2\end{aligned}`

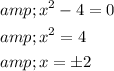
Now, substitute these values of x back into the equation for the parabolic path to find the corresponding y values:

For x=2:

`y=(2)^2-4=0`

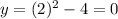
So, one intersection point is (2,0).

For x=−2:

`y=(-2)^2-4=0`

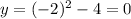
So, the other intersection point (−2,0).

Question:

A planet follows an elliptical path described by
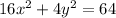`16 x^2+4 y^2=64`. A comet follows the parabolic path
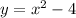`y=x^2-4`. where might the comet intersect the orbiting planet?