The area of the region bounded by the graph of
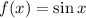 and the x-axis on the interval
and the x-axis on the interval
![\([- (\pi)/(3), (2\pi)/(3)]\)](https://img.qammunity.org/2024/formulas/mathematics/high-school/7f7iw5tv90v6arh3g7bpp08kxqxgpf3qnj.png) is indeed 1 square unit.
is indeed 1 square unit.
To find the area of the region bounded by the graph of
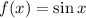 and the x-axis on the interval
and the x-axis on the interval
![\([- (\pi)/(3), (2\pi)/(3)]\)](https://img.qammunity.org/2024/formulas/mathematics/high-school/7f7iw5tv90v6arh3g7bpp08kxqxgpf3qnj.png) , we can visualize the region by sketching the graph of
, we can visualize the region by sketching the graph of
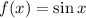 within this interval.
within this interval.
The graph of
 is a periodic function that oscillates between -1 and 1 as
is a periodic function that oscillates between -1 and 1 as
 varies. The given interval
varies. The given interval
![\([- (\pi)/(3), (2\pi)/(3)]\)](https://img.qammunity.org/2024/formulas/mathematics/high-school/7f7iw5tv90v6arh3g7bpp08kxqxgpf3qnj.png) captures a portion of this oscillation.
captures a portion of this oscillation.
Let's visualize the graph:
- At
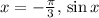 is positive, and the graph rises.
is positive, and the graph rises.
- At
 , the function crosses the x-axis.
, the function crosses the x-axis.
- At
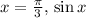 is again positive, and the graph rises once more.
is again positive, and the graph rises once more.
- At
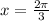 , the function crosses the x-axis again.
, the function crosses the x-axis again.
Now, within this interval, the shaded region represents the area between the curve
 and the x-axis. To find this area, we set up the definite integral:
and the x-axis. To find this area, we set up the definite integral:
![\[ \int_{-(\pi)/(3)}^{(2\pi)/(3)} \sin x \, dx \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/o76qo3devmdyy3q0qg6hsrqjbpqwkbgp6h.png)
The integral of
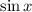 is
is
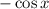 , so applying the Fundamental Theorem of Calculus, we evaluate:
, so applying the Fundamental Theorem of Calculus, we evaluate:
![\[ \left[ -\cos x \right]_{-(\pi)/(3)}^{(2\pi)/(3)} \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/2e1vnnii0z0abem7tbncuhc9fv55eyypew.png)
Plugging in the upper and lower limits:
![\[ -\cos\left((2\pi)/(3)\right) + \cos\left(-(\pi)/(3)\right) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/h6gcuuqrpm88mdj4w7axdgcp1o9s5qffqu.png)
Evaluating these cosine values:
![\[ -\left(-(1)/(2)\right) + (1)/(2) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/9i2wfkcf1u2aqjugbo535rqb6h0jg1fbfu.png)
Simplifying:
![\[ (1)/(2) + (1)/(2) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/lybx8g6mlcxzluf4fzrmhrio5wptow3s52.png)
Which equals 1.