Question

Which of the following correctly demonstrates the associative property of addition ?

A. x •( y+z) = (x•y) + z.
B. m•(x•y) = (m•x)•y
C. (x+y) + z+r= x+ (y+z)+r
D. y-(x+1) = (y-x)+ 1

Answer 1

`\sf\textsf{ Answer is: C.} \: \sf (x + y) + z + r = x + (y + z) + r`

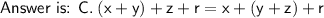
Explanation:

The associative property of addition states that the grouping of numbers within parentheses, when adding, does not affect the result of the addition.

In other words, for any three numbers a, b, and c is:

`\sf (a + b) + c = a + (b + c)`

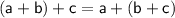
Now, let's examine the given options:

• 
  `\sf A. \: x \cdot (y + z) = (x \cdot y) + z:`
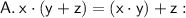
  This is not an example of the associative property of addition; it appears to involve multiplication, not addition.

• 
  `\sf B. m \cdot (x \cdot y) = (m \cdot x) \cdot y:`
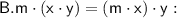
  This is not an example of the associative property of addition; it involves multiplication, not addition.

• 
  `\sf C. (x + y) + z + r = x + (y + z) + r:`
  This is an example of the associative property of addition. It demonstrates that you can change the grouping of the numbers without affecting the sum.

• 
  `\sf D. y - (x + 1) = (y - x) + 1:`
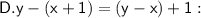
  This is not an example of the associative property of addition; it involves subtraction and addition, not just addition.

So, the correct answer is C:

`\sf (x + y) + z + r = x + (y + z) + r`