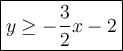Question

Which inequality is represented by the graph?

a. yくー 3/2x-2
b. y≥-3/2x-2
c. y> -3/2x-2
d. y≤-3/2x-2

(I know the the answer is b, I need someone to work out the problem for me!)​

Answer 1

`\textsf{b)} \quad y\geq-(3)/(2)x-2`

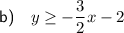
Explanation:

To find the inequality that is represented by the given graph, we first need to determine the equation of the boundary line.

To do this, identify two points on the line:

• Point 1: (x₁, y₁) = (-2, 1)
• Point 2: (x₂, y₂) = (0, -2)

Substitute the points into the slope formula to find the slope of the boundary line:

`\textsf{Slope}\;(m)=(y_2-y_1)/(x_2-x_1)=(-2-1)/(0-(-2))=(-3)/(0+2)=-(3)/(2)`

Substitute the slope and one of the points into point-slope form of a linear equation:

`\begin{aligned}y-y_1&=m(x-x_1)\\\\y-(-2)&=-(3)/(2)(x-0)\\\\y+2&=-(3)/(2)x\\\\y&=-(3)/(2)x-2\end{aligned}`

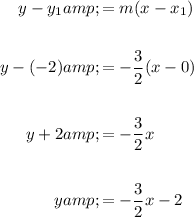
Therefore, the equation of the boundary line is:

`y=-(3)/(2)x-2`

When graphing inequalities:

• < or > : dashed line.
• ≤ or ≥ : solid line.
• < or ≤ : shade under the line.
• > or ≥ : shade above the line.

As the boundary line is solid and the shading is above the line, replace the equality sign with the inequality sign ≥.

Therefore, the inequality that is represented by the graph is:

`\large\boxed{y\geq-(3)/(2)x-2}`