Question

Chemical Fertilizer Centre sells 240,000 bags of lawn fertilizer annually. The

optimal safety stock (Which is on hand initially) is 1,500 bags. Each bag costs
centre Rs. 8, inventory-carrying costs are 20 percent, and the cost of placing
an order with its suppliers is Rs. 25.
a) What is the economic order quantity?
b) What is the maximum inventory of fertilizer?
c) What is Centre's average inventory?
d) How often must the Centre order?

Answer 1

To solve this problem, we can use the Economic Order Quantity (EOQ) formula and related inventory management formulas. Let's go through each part of the problem:

a) Economic Order Quantity (EOQ):

The EOQ formula is given by:

`EOQ=\sqrt[]{(2DS)/(H) }`

Where:

• 
  `D` = Annual demand (240,000 bags)
• 
  `S` = Ordering cost per order (Rs. 25)
• 
  `H` = Holding cost per unit per year (20% of Rs. 8)​

Substitute the values into the formula:

​
`EOQ=\sqrt[]{2}`×
`240,000`×
`25`

`\frac{}{0.20}`×
`8`

`EOQ` ≈
`1,848.81`

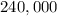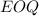So, the economic order quantity is approximately 1,848.81 bags.

b) Maximum Inventory:

The maximum inventory can be calculated using the EOQ formula:

`Maximum Inventory = EOQ + Safety Stock`

`Maximum Inventory = 1,848.81 + 1,500`

`Maximum Inventory=3,348.81`

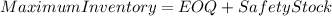
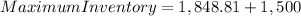
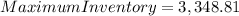
The maximum inventory of fertilizer is approximately 3,348.81 bags.

c) Average Inventory:

The ordering frequency (also known as reorder point) can be calculated using the EOQ formula and the annual demand:

`Ordering Frequency = (Annual Demand)/(EOQ)`

`Ordering Frequency = (240,000)/(1,848.81)`

`Ordering Frequency` ≈
`129.84`

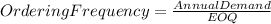
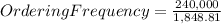
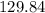
So, the Centre must order approximately every 130 times a year.