Question

How do you do the graph

Answer 1

x = number of hours babysitting

y = number of hours gardening

10x = amount of money made from babysitting

5y = amount of money made from gardening

10x+5y = total amount of money made from both jobs

The equation 10x+5y = 80 represents the idea of Charlene making exactly $80 total from both jobs combined. This will be one of the boundary lines we graph.

Let's solve for y.

10x+5y = 80

5(2x+y) = 80

2x+y = 80/5

2x+y = 16

y = -2x+16

Compare that to the template y = mx+b

m = -2 = slope

b = 16 = y intercept

The y intercept of 16 tells us that (0,16) is one point on the line.

Another point is (1,14) after following the slope directions of "down 2, right 1". Think of m = -2 as m = -2/1.

Therefore, the line goes through (0,16) and (1,14) as shown in the diagram below.

----------------------

x = number of hours babysitting

y = number of hours gardening

x+y = total number of hours

If Charlene works exactly 12 hours total, then x+y = 12

This solves to y = -x+12

Two points on this second line are (0,12) and (1,11)

The graph is shown below.

-----------------------

To recap so far we have this system of linear equations

`\begin{cases}10x+5y = 80\\x+y = 12\end{cases}`

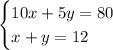
Each equation is before we isolated y.

We're told that Charlene wants to earn "at least $80". So she wants $80 or more. This would mean points on the boundary 10x+5y = 80 (aka y = -2x+16) or points above this boundary are valid solutions. We shade above the solid boundary line 10x+5y = 80 to indicate this.

At the same time, she has time constraints. She cannot work more than 12 hours. We must consider points on x+y = 12 or points below it. Shade below the solid boundary line x+y = 12.

The overlapping shaded regions results in what is shaded in blue shown below. Points on the boundary lines are valid solutions as long as they are adjacent to the blue region.

Take note that
`x \ge 0 \ \text{ and } \ y \ge 0` since it doesn't make sense to have a negative number of hours. Therefore, we focus on the upper right quadrant only.

Any point in this blue shaded region is a solution. For example the point (9,2) is a solution. A point like (8,4) is a solution because it's on the boundary and adjacent to the blue region.

A non-solution is (2,10) even though this point is on a boundary. Note how this point is not adjacent to the blue shaded region. This means (2,10) makes one condition true but the other is false. Both conditions need to be true.