Question

Where does the graph of the function Y=tan(x) have asymptotes?​

Answer 1

`\text{x} = (\pi)/(2)+2\pi n \ \text{ and } \ \text{x} = (3\pi)/(2)+2\pi n \\\text{where n is an integer}`

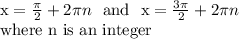
I'm working in radian mode which is what many calculus classes use.

=============================================

Explanation

Tangent is the ratio of sine over cosine.

`\tan(\text{x})=\frac{\sin(\text{x})}{\cos(\text{x})}`

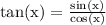
Vertical asymptotes occur when the denominator is zero. This is because of a division by zero error. Something like 1/0 is not allowed.

The question then becomes: When is cos(x) = 0 true?

Use the unit circle to see that cos(x) = 0 when x = pi/2 radians and x = 3pi/2 radians. In other words: cos(pi/2) = 0 and cos(3pi/2) = 0

This means tan(x) has vertical asymptotes at x = pi/2 and x = 3pi/2

We add 2pi*n to each item because of coterminal angles. This will encapsulate all of the infinitely many solutions. The variable n is any integer.

Use a graphing tool like GeoGebra, Desmos, or similar to help visually verify that we have the correct vertical asymptotes. Make sure to set things to radian mode.

Tan(x) does not have any horizontal asymptotes, nor any oblique asymptotes.

Side notes:

• pi/2 radians = 90 degrees
• 3pi/2 radians = 270 degrees
• 2pi radians = 360 degrees

Answer 2

x = 180° × n, for integer n.

x = πn, for integer n.

Explanation:

tan x = sin x / cos x

Where cos x has value of zero, there is a discontinuity in the function y = tan x, and there is an asymptote at that x value.

Using degrees:

cos x = 0 at x = 180° × n, for all integers n.

Using radians:

cos x = 0 at x = πn, for all integers n.