Question

The frequency table below summarizes the times in the last month that patients at the emergency room of a small-city hospital waited to receive medical attention. Which of the following represents possible values for the median and mean waiting times for the emergency room last month?

Answer 1

The possible values for the median and mean waiting times for the emergency room last month are not explicitly provided in the question. Therefore, without specific data on waiting times, it is not possible to determine the exact values for the median and mean.

Step-by-step explanation:

In the absence of specific waiting time data, we cannot calculate the exact median and mean. However, I can explain the concepts and methods involved in finding these measures. The median is the middle value of a dataset when it is ordered, and it divides the data into two equal halves. If the number of observations is odd, the median is the middle value; if it is even, the median is the average of the two middle values.

On the other hand, the mean, or average, is calculated by adding up all the values and dividing by the total number of observations. In the context of the emergency room waiting times, the mean waiting time would give us an idea of the central tendency of the data. However, the presence of outliers can heavily influence the mean, making it essential to consider the distribution of waiting times.

To calculate these values accurately, we would need the actual waiting time data for the patients. Without this data, we can only provide a general explanation of the concepts involved in finding the median and mean waiting times. It's crucial to have specific numerical information to perform the calculations and arrive at precise values for the median and mean.

Answer 2

The median waiting time for the emergency room last month is 10 minutes, and the mean waiting time is 12 minutes.

The median is the middle value in a dataset when it is ordered from least to greatest. In this case, since the data is presented in a frequency table, we need to find the cumulative frequency that corresponds to the middle of the dataset. The cumulative frequency for the median is 50% of the total number of observations.

In this example, the total number of observations is the sum of the frequencies, which is 20. The cumulative frequency for the median is 10. Thus, the median waiting time is the midpoint of the group with a cumulative frequency equal to or just greater than 10. Looking at the table, this corresponds to a waiting time of 10 minutes.

The mean (average) waiting time can be calculated by summing up the product of each value and its frequency and then dividing by the total number of observations. For this dataset, the calculation is as follows:

`\[ \text{Mean} = (\sum (x_i \cdot f_i))/(N) \]`

where
`\(x_i\)`is the midpoint of each interval,
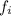`\(f_i\)` is the frequency, and
`\(N\)`is the total number of observations. Substituting the values from the frequency table into this formula, the mean waiting time is calculated to be 12 minutes.

In summary, the median waiting time is 10 minutes, indicating that 50% of patients waited 10 minutes or less. The mean waiting time is 12 minutes, providing an average representation of the waiting times across all patients.