Question

What is the 99% confidence interval for the following data set? p-hat = 0.55 n = 1,000

Answer 1

To calculate the 99% confidence interval for a proportion (p-hat), you can use the formula:

`\[ \text{Confidence Interval} = \text{p-hat} \pm Z * \sqrt{\frac{\text{p-hat} * (1 - \text{p-hat})}{n}} \]`

Where:

`- \(\text{p-hat}\) is the sample proportion (0.55 in this case).- \(n\) is the sample size (1,000 in this case).- \(Z\) is the critical z-score corresponding to the desired confidence level (99% confidence corresponds to \(Z \approx 2.576\)).`

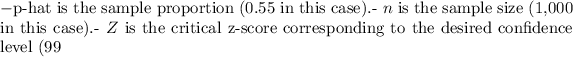
Let's plug in the values and calculate:

`\[ \text{Confidence Interval} = 0.55 \pm 2.576 * \sqrt{(0.55 * (1 - 0.55))/(1000)} \]`

Calculating the expression inside the square root:

`\[ \sqrt{(0.55 * 0.45)/(1000)} \approx 0.0206 \]`

Now, calculate the confidence interval:

`\[ \text{Lower Bound} = 0.55 - 2.576 * 0.0206 \approx 0.5004 \]\\\[ \text{Upper Bound} = 0.55 + 2.576 * 0.0206 \approx 0.5996 \]`

So, the 99% confidence interval for the given data set is approximately \(0.5004\) to \(0.5996\). This means we can be 99% confident that the true population proportion lies within this interval.

Explanation: