- The function
 has a greater average rate of change between
has a greater average rate of change between
 and
and

- The second part cannot be determined without additional information or a clearer view of the graph.
- The function f and g have the same average rate of change between x =0 and x=1.5
The average rate of change of a function over an interval is the change in the function's value divided by the change in the input value (often the change in
 divided by the change in
divided by the change in
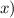 over that interval. It is essentially the slope of the secant line between two points on the function's graph.
over that interval. It is essentially the slope of the secant line between two points on the function's graph.
1. Average rate of change between
 and
and
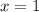 :
:
- The function
 has a smaller slope than function
has a smaller slope than function
 between
between
 and
and
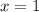 . This can be observed because \( g \) increases more rapidly than \( f \) over this interval.
. This can be observed because \( g \) increases more rapidly than \( f \) over this interval.
- Therefore, the function
 has a greater average rate of change between
has a greater average rate of change between
 and
and

2. Average rate of change between
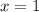 and
and

- Without specific values, we can only make a qualitative analysis based on the steepness of the curve.
- If the trend that
 increases faster than
increases faster than
 continues beyond
continues beyond
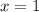 , then
, then
 would still have a greater average rate of change between
would still have a greater average rate of change between
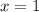 and
and
 . However, we cannot confirm this without more information or a clearer view of the functions beyond
. However, we cannot confirm this without more information or a clearer view of the functions beyond
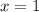 .
.
3. The same average rate of change:
both function f and g intersect at x =0 and x=1.5
Such that , f(1.5) = g(1.5)
and f(0) = g(0)
Hence the function f and g have the same average rate of change between x =0 and x=1.5
- The function
 has a greater average rate of change between
has a greater average rate of change between
 and
and

- The second part cannot be determined without additional information or a clearer view of the graph.
- The function f and g have the same average rate of change between x =0 and x=1.5