Question

Calculus help please

Answer 1

Answer: -4

============================================

Step-by-step explanation

Plug in t = -1

`P(t) = 2t^2 - 2\\\\P(-1) = 2(-1)^2 - 2\\\\P(-1) = 0\\\\`

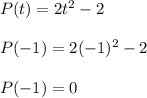
Repeat for something close to -1. Let's say we go for t = -1.5

`P(t) = 2t^2 - 2\\\\P(-1.5) = 2(-1.5)^2 - 2\\\\P(-1.5) = 2.5\\\\`

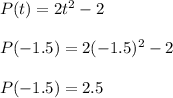
Compute the average rate of change from t = -1.5 to t = -1

`(P(a)-P(b))/(a-b)\\\\(P(-1.5)-P(-1))/(-1.5-(-1))\\\\(2.5-0)/(-1.5+1)\\\\(2.5)/(-0.5)\\\\-5\\\\`

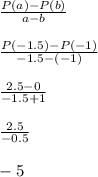
The average rate of change from t = -1.5 to t = -1 is -5.

This is the slope of the secant line through (-1,0) and (-1.5, 2.5)

-----------------

The idea is then to pull the t = -1.5 value closer to t = -1. We'll keep t = -1 fixed in place.

What happens if we tried something like t = -1.2?

`P(t) = 2t^2 - 2\\\\P(-1.2) = 2(-1.2)^2 - 2\\\\P(-1.2) = 0.88\\\\`

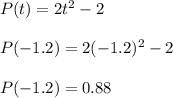
Let's calculate the new average rate of change.

`(P(a)-P(b))/(a-b)\\\\(P(-1.2)-P(-1))/(-1.2-(-1))\\\\(0.88-0)/(-1.2+1)\\\\(0.88)/(-0.2)\\\\-4.4\\\\`

-----------------

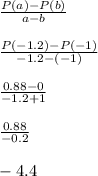
Now let's try t = -1.1

`P(t) = 2t^2 - 2\\\\P(-1.1) = 2(-1.1)^2 - 2\\\\P(-1.1) = 0.42\\\\\text{Then compute the average rate of change }\\\\(P(a)-P(b))/(a-b)\\\\(P(-1.1)-P(-1))/(-1.2-(-1))\\\\(0.42-0)/(-1.1+1)\\\\(0.42)/(-0.1)\\\\-4.2\\\\`

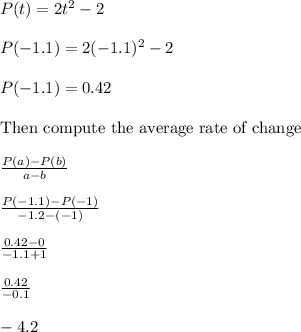
We seem to be approaching a fixed value of -4 point something. Perhaps -4.2 or maybe -4.1

------------------

If we keep up this process, then we have this table

`\begin{array}c \cline{1-3}\text{a} & \text{P(a)} & \text{AROC from t = a to t = -1}\\\cline{1-3}-1.5 & 2.5 & -5\\\cline{1-3}-1.2 & 0.88 & -4.4\\\cline{1-3}-1.1 & 0.42 & -4.2\\\cline{1-3}-1.05 & 0.205 & -4.1\\\cline{1-3}-1.005 & 0.02005 & -4.01\\\cline{1-3}-1.0005 & 0.0020005 & -4.001\\\cline{1-3}-1.00005 & 0.000200005 & -4.0001\\\cline{1-3}\end{array}\\\\\text{AROC = average rate of change}`

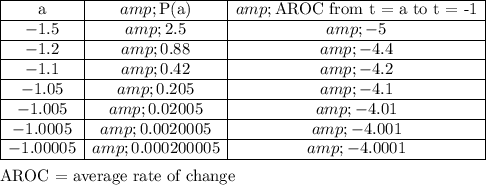
It appears we're getting closer and closer to an instantaneous rate of change of -4.

Let's look at a table where we approach t = -1 from the opposite side. I'll start at something like t = 0 and move to the left.

Here's a table of select values.

`\begin{array}c \cline{1-3}\text{b} & \text{P(b)} & \text{AROC from t = -1 to t = b}\\\cline{1-3}0 & -2 & -2\\\cline{1-3}-0.5 & -1.5 & -3\\\cline{1-3}-0.9 & -0.38 & -3.8\\\cline{1-3}-0.99 & -0.0398 & -3.98\\\cline{1-3}-0.999 & -0.003998 & -3.998\\\cline{1-3}-0.9999 & -0.00039998 & -3.9998\\\cline{1-3}-0.99999 & -0.0000399998 & -3.99998\\\cline{1-3}\end{array}`

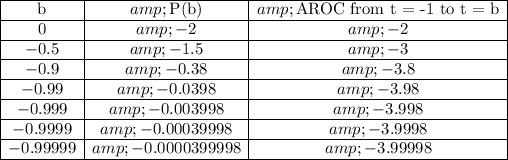
There might be some (slight) rounding error happening. I'm not entirely sure.

But what I'm sure about is the tangent line slope is indeed -4. We can use the derivative to verify this claim.

Luckily both tables have the AROC slowly approach -4 from either side of t = -1.

So a good estimate of the slope of the tangent would be -4. But if you used less precision in the tables, then perhaps you would arrive at something close to -4 but not -4 itself. Feel free to explore other values close to -1.

I recommend using spreadsheet software to help make crunching the numbers easier.