Question

Answer the question precisely and thoroughly

Answer 1

(a) 12 ± 0.33 cm (11.67 ≤ x ≤ 12.33)

(b) 'Delta (δ)' is associated with the allowable variance in side lengths, while 'epsilon (ε)' pertains to the tolerance in area.

(c) The ideal side length would be represented by 'a' and the area would be denoted by 'L'

Explanation:

The question aims to understand the precision required in cutting a square piece of Aerogel with an acceptable error tolerance in its area. To answer these questions, we will make use of the Delta-Epsilon definition of limits to find out how accurately the side lengths must be cut. We will also explain how these numbers relate to δ & ϵ, a & L.

`\hrulefill`

(a) Accuracy in Side Length
`\hrulefill`

Using the delta-epsilon definition, we'll determine the accuracy with which the engineer must cut the side length of the square of Aerogel by establishing a relationship between a small change in side length (delta) and the resultant change in area (epsilon).

Recall,
`\boxed{\begin{minipage}{\linewidth}The limit of \( f(x) \) as \( x \) approaches \( a \) is \( L \), denoted as:\[\lim_{{x \to a}} f(x) = L\]This is formally given by the \(\delta-\epsilon\) criterion as follows:\[\forall \epsilon > 0, \ \exists \delta > 0, \ \forall x \in \text{Domain}(f), \quad \sigma < |x - a| < \delta \implies |f(x) - L| < \epsilon\]\end{minipage}}`

We are given:

• L = 144 cm²
• a = 12 cm [∵ √144 = 12]
• ε = 8 cm²
• f(x) = x²

We have to find 'δ'. We have:

`\bullet \ f(x)=x^2 \ \text{and} \ \lim_(x \to 12) f(x)=L=144\\\\\\\bullet \ \sigma < |x - a| < \delta \ \text{and} \ |f(x) - L| < \epsilon\\\\\\\\\implies |x^2 - 144| < 8\\\\\\\\\implies |(x-12)(x+12)| < 8\\\\\\\\\implies |x-12|(12+12) < 8\\\\\\\\\implies 24|x-12| < 8\\\\\\\\\implies |x-12| < (8)/(24) \\\\\\\\\implies |x-12| < (8)/(24) \\\\\\\\\implies |x-12| < (1)/(3) \\\\\\\\\therefore \boxed{\delta = (1)/(3) \approx 0.33} \ \ \big(\because |x-12| < \delta \big)`

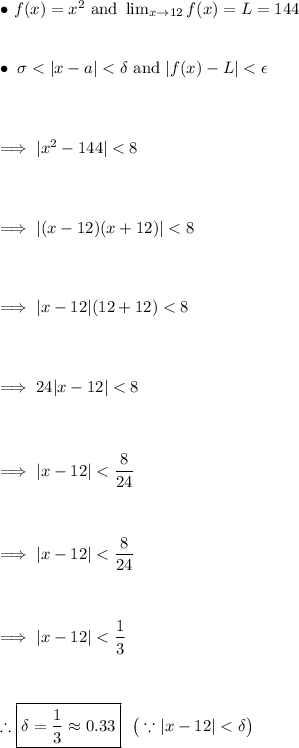
Thus, the engineer must cut each side to be 12 ± 0.33 cm in order to maintain an area within the tolerance of 8 cm².

`\hrulefill`

(b) Relation to δ and ϵ
`\hrulefill`

The numbers calculated for the accuracy in the area and side length directly relate to the δ and ϵ used in limit theory.

In the context of limits, ϵ represents the tolerance around the limit value (in this case, the area), and δ is the tolerance around the value where the limit is evaluated (in this case, the side length). Here, ϵ = 8 cm² for the area, and δ = 0.67 cm for the side length.

`\hrulefill`

(c) Relation to a and L
`\hrulefill`

The given square area and its corresponding side length relate to 'a' and 'L', which are standard variables used to denote the point of interest and the limit, respectively, in limit theory.

In the context of limits, 'a' represents the point in the domain where we are investigating the behavior of a function, and 'L' represents the limit or the value that the function approaches as its argument approaches 'a'. In this problem, 'a' would be the ideal side length of 12 cm, and 'L' would be the area 144 cm². These are the values that the measurements are supposed to be centered around.