Answer: Both isosceles and right triangle
=================================================
Step-by-step explanation
I'll label the 3 points as A,B,C.
A = (-2,-5)
B = (0,15)
C = (9,4)
Let's find the distance from A to B. It's the same as finding the length of segment AB.
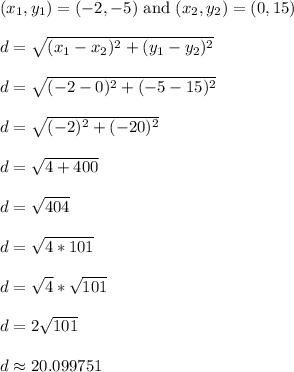
Segment AB is exactly
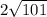 units long.
units long.
Segment AB is approximately 20.099751 units long.
If you follow similar steps then you'll find that segment BC is
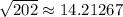 units long. The same will apply to segment AC.
units long. The same will apply to segment AC.
Therefore, BC = AC and it proves the triangle is isosceles
--------------
To prove if we have a right triangle or not, we'll need to find the slopes of AB, BC and AC
I'll show the steps how to find the slope of line through A(-2,-5) and B(0,15).

Line AB has slope 10.
I'll skip steps, but line BC has slope -11/9
While slope AC is 9/11
The slopes of BC and AC are negative reciprocals of one another. They multiply to -1; which means AC and BC are perpendicular. Therefore, triangle ABC is a right triangle.
----------------
Conclusion: Triangle ABC is an isosceles right triangle