Question

Given f(x)= 2(x-3)^2-6

The graph of f(x) has two real zeros. Notice that a zero of the function occurs between x=4 and x=5. Use computations to justify why a zero of the function must exist at some x-value on this interval 4 is less than or equal to x is less than or equal to five. ​

Answer 1

Plug in x = 4

`f(x) = 2(x-3)^2-6\\\\f(4) = 2(4-3)^2-6\\\\f(4) = 2(1)^2-6\\\\f(4) = 2(1)-6\\\\f(4) = 2-6\\\\f(4) = -4\\\\`

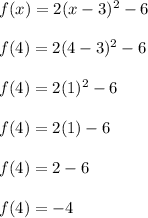
The result itself doesn't matter. All we care about is whether the result is positive or negative. In this case, it's negative.

Now plug in x = 5

`f(x) = 2(x-3)^2-6\\\\f(5) = 2(5-3)^2-6\\\\f(5) = 2(2)^2-6\\\\f(5) = 2(4)-6\\\\f(5) = 8-6\\\\f(5) = 2\\\\`

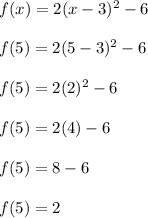
We get a positive result this time.

The f(x) output changing from negative to positive must mean f(x) = 0 at least once in the interval 4 < x < 5

Think of the function curve acting like a road. The road starts off in negative territory. Let's say it's south of the border of whatever country you prefer. Being in positive territory means you're now north of the border.

Going from "south of the border" to "north of the border" must mean you crossed the border itself at least once. Each border crossing refers to an x intercept aka root. The border is the x axis.

For more information, search out "intermediate value theorem". Also feel free to ask me further questions if you're still stuck.