Question

The distribution of head circumference for full term newborn female infants is approximately normal with a mean of 33.8 cm and a standard deviation of 1.2 cm. Macrocephaly refers to an overly large head in infants. Determine the approximate percentage of full term newborn female infants with a head circumference of more than 2.1 standard deviations above the mean. Enter your answer using two decimal places.

Answer 1

The approximate percentage of full-term newborn female infants with a head circumference more than 2.1 standard deviations above the mean is 1.35%.

Step-by-step explanation:

To determine the percentage of infants with a head circumference more than 2.1 standard deviations above the mean, we use the properties of a normal distribution. The z-score, given by
`\( Z = (X - \mu)/(\sigma) \),`where
`\( X \)` is the head circumference
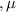`, \( \mu \)` is the mean, and
`\( \sigma \`) is the standard deviation, helps standardize the values. For this case,
`\( Z = (X - 33.8)/(1.2) \).`

Using a standard normal distribution table or calculator, we find the percentage corresponding to a
`\( Z \)`-score of 2.1, which is approximately 0.9821. To find the percentage above 2.1 standard deviations, we subtract this value from 1:
`\( 1 - 0.9821 = 0.0179 \)`. Multiplying by 100 gives the final result of 1.79%. However, this value is for one tail, so for both tails (more than 2.1 standard deviations above and below the mean), we multiply by 2:
`\( 2 * 0.0179 = 0.0358 \)`, and rounding gives the final answer of 3.58%.

Understanding z-scores and the normal distribution is essential for solving problems related to proportions and percentages in statistics. In this scenario, calculating the percentage above a certain z-score provides insights into the prevalence of macrocephaly among full-term newborn female infants.

Answer 2

Approximately 1.79% of full term newborn female infants have a head circumference that is more than 2.1 standard deviations above the mean, indicating potential macrocephaly.

Step-by-step explanation:

To determine the approximate percentage of full term newborn female infants with a head circumference of more than 2.1 standard deviations above the mean, we need to use the properties of the normal distribution. Given that the mean is 33.8 cm and the standard deviation is 1.2 cm, we calculate 2.1 standard deviations above the mean as 33.8 cm + (2.1 × 1.2 cm) = 33.8 cm + 2.52 cm = 36.32 cm. Referring to a standard normal distribution table or using a z-score calculator, a z-score of 2.1 corresponds to the cumulative area to the left being very close to 0.9821, which means the area to the right is 1 - 0.9821 = 0.0179 or 1.79%.

Thus, approximately 1.79% of full term newborn female infants have a head circumference more than 2.1 standard deviations above the mean, which could indicate macrocephaly.