Question

A point on the x-axis that is equidistant from the points (8,-10) and (-4,9) is

i need help, please ​

Answer 1

Answer: (67/24, 0)

67/24 = 2.791667 approximately

=====================================================

Step-by-step explanation

The mystery point is of the form (x,0) where x is some real number. Likely it's some number between -4 and 8 which are the x coordinates of the given points.

We know the y coordinate is 0 because this mystery point is on the x-axis.

Let's compute the distance from (8,-10) to (x,0)

`(x_1,y_1) = (8,-10) \text{ and } (x_2, y_2) = (x,0)\\\\d = √((x_1 - x_2)^2 + (y_1 - y_2)^2)\\\\d = √((8-x)^2 + (-10-0)^2)\\\\d = √((8-x)^2 + (-10)^2)\\\\d = √((x^2-16x+64) + 100)\\\\d = √(x^2-16x+164)\\\\`

Then we'll need the distance expression from (x,0) to (-4,9)

`(x_1,y_1) = (x,0) \text{ and } (x_2, y_2) = (-4,9)\\\\d = √((x_1 - x_2)^2 + (y_1 - y_2)^2)\\\\d = √((x-(-4))^2 + (0-9)^2)\\\\d = √((x+4)^2 + (0-9)^2)\\\\d = √((x^2+8x+16) + 81)\\\\d = √(x^2+8x+97)\\\\`

If the mystery point (x,0) is equidistant from (8,-10) and (-4,9), then those distance expressions we just calculated must be equal to one another.

`√(x^2-16x+164) = √(x^2+8x+97)\\\\(√(x^2-16x+164))^2 = (√(x^2+8x+97))^2\\\\x^2-16x+164 = x^2+8x+97\\\\-16x+164 = 8x+97\\\\-16x-8x = 97-164\\\\-24x = -67\\\\x = (-67)/(-24)\\\\x = (67)/(24)\\\\x \approx 2.791667\\\\`

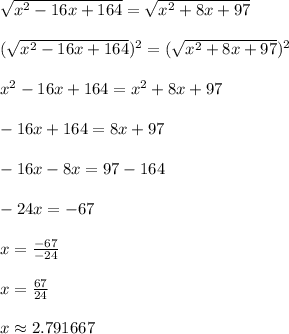
Therefore the mystery point is located at approximately (2.791667, 0)

Round that approximate value however needed.

I recommend using GeoGebra to help verify the answer.