Question

Match each expression on the left with (x²-3x-18)-:(x-6) (x³-x²-5x-3)-:(x²+2x+1) (x³+2x^(2)-1)-:(x²+x+1)

Answer 1

Match each expression on the left with the corresponding quotient on the right as follows:

`1. \( (x^2 - 3x - 18)/(x - 6) \)2. \( (x^3 - x^2 - 5x - 3)/(x^2 + 2x + 1) \)3. \( (x^3 + 2x^2 - 1)/(x^2 + x + 1) \)`

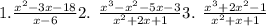
Step-by-step explanation:

To match each expression on the left with its corresponding quotient, we need to perform the division indicated by the given expressions. Let's evaluate each one:

1.
`\( (x^2 - 3x - 18)/(x - 6) \):`

This is a simple polynomial division where x - 6 divides
`\( x^2 - 3x - 18 \)`. The result is x + 2, so the first expression matches with x + 2.

2.
`\( (x^3 - x^2 - 5x - 3)/(x^2 + 2x + 1) \):`

Here,
`\( x^2 + 2x + 1 \) divides \( x^3 - x^2 - 5x - 3 \)`. The result is x - 3 , so the second expression matches with x - 3

3.
`\( (x^3 + 2x^2 - 1)/(x^2 + x + 1) \):`

This involves dividing
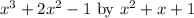`\( x^3 + 2x^2 - 1 \) by \( x^2 + x + 1 \)`. The quotient is x + 1, so the third expression matches with x+1.

Understanding polynomial division is crucial to finding the quotients. In each case, the divisor is a factor of the numerator, resulting in a simple polynomial expression. Matching the given expressions with their respective quotients involves recognizing the factors and performing the division accurately.

In summary, the matching expressions are:

`1. \( (x^2 - 3x - 18)/(x - 6) \) matches with \( x + 2 \).\\2. \( (x^3 - x^2 - 5x - 3)/(x^2 + 2x + 1) \) matches with \( x - 3 \).\\3. \( (x^3 + 2x^2 - 1)/(x^2 + x + 1) \) matches with \( x + 1 \).`