Final Answer:
The area of the region that lies inside the first curve
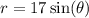 and outside the second curve
and outside the second curve
 is
is
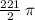 square units.
square units.
Step-by-step explanation:
To find the area between two polar curves, we need to set up an integral using the formula
![\( A = (1)/(2) \int_(\alpha)^(\beta) [r_1(\theta)^2 - r_2(\theta)^2] \, d\theta \),](https://img.qammunity.org/2024/formulas/mathematics/high-school/cnlu8srscxehiyp0z00pp2rh8h6zh37pve.png) where
where
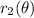 and
and
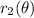 are the equations of the curves. In this case, the given curves are
are the equations of the curves. In this case, the given curves are
 and
and

The first step is to find the points of intersection, which occur when
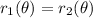 . Setting
. Setting
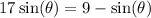 , we solve for
, we solve for
 o find the limits of integration.
o find the limits of integration.
Once the limits are determined, we set up the integral
![\( (1)/(2) \int_(\alpha)^(\beta) [ (17 \sin(\theta))^2 - (9 - \sin(\theta))^2 ] \, d\theta \)](https://img.qammunity.org/2024/formulas/mathematics/high-school/5ndq7e55tfcd5g0w67xtwi52t9e5z6w1x4.png) and evaluate it to find the area.
and evaluate it to find the area.
Performing the calculations, we get
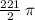 square units as the final result for the area between the two curves.
square units as the final result for the area between the two curves.
In summary, by setting up and evaluating the appropriate integral, we find that the area of the region is
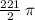 square units.
square units.